A 14 Foot Ladder Is Leaning Against A Building
A 14 Foot Ladder Is Leaning Against A Building - How high up on the building will the top of the ladder reach? Ot drawn to scale which expression can be used to find the height, h, in. A 14 foot ladder is leaning against a building. The ladder makes a 50° angle with the ground as shown in the diagram. There are 2 steps to solve this one. How high is the top of the ladder from the ground? To find out how far away the base of the ladder is from the building, we can use the pythagorean theorem. This theorem applies to right triangles and states that: A 14 foot ladder is leaning against a building. This setup forms a right triangle where: A 14 foot ladder is leaning against a building. This theorem applies to right triangles and states that: How high is the top of the ladder from the ground? The ladder makes a 50° angle with the ground as shown in the diagram. How high up the building will the ladder reach? The angle created by the ladder and the building is 22 degrees. 28 square root of 2 feet b. The base of the ladder is 4 feet from the building. A is one leg of. Trigonometric ratio is used to show the relationship between the sides and angles of a right angled triangle. The angle created by the ladder and the building is 22 degrees. This theorem applies to right triangles and states that: This setup forms a right triangle where: 28 square root of 2 feet b. A is one leg of. This theorem applies to right triangles and states that: A 14 foot ladder is leaning against a building. This setup forms a right triangle where: There are 2 steps to solve this one. A is one leg of. There are 2 steps to solve this one. How high up on the building will the top of the ladder reach? The angle created by the ladder and the building is 22 degrees. 28 square root of 2 feet b. This setup forms a right triangle where: How high up on the building will the top of the ladder reach? To find out how far away the base of the ladder is from the building, we can use the pythagorean theorem. Find the rate at which the area is changing at the instant the radius is 16 feet when the radius is 16 feet, the area is. Find the rate at which the area is changing at the instant the radius is 16 feet when the radius is 16 feet, the area is changing at approximately square feet per minute (round to the nearest. There are 2 steps to solve this one. The ladder makes a 50° angle with the ground as shown in the diagram. 28. This setup forms a right triangle where: This theorem applies to right triangles and states that: The base of the ladder is 4 feet from the building. A 14 foot ladder is leaning against a building. The angle created by the ladder and the building is 22 degrees. How high up on the building will the top of the ladder reach? The ladder makes a 50° angle with the ground as shown in the diagram. If the bottom of the ladder is sliding along the pavement directly away from the building at 2 feet/second, how fast is the top of the ladder. We want to find out how. How high up on the building will the top of the ladder reach? A is one leg of. Trigonometric ratio is used to show the relationship between the sides and angles of a right angled triangle. How high up the building will the ladder reach? 28 square root of 2 feet b. Find the rate at which the area is changing at the instant the radius is 16 feet when the radius is 16 feet, the area is changing at approximately square feet per minute (round to the nearest. If the bottom of the ladder is sliding along the pavement directly away from the building at 2 feet/second, how fast is the. At approximately what height does the ladder touch the building? Ot drawn to scale which expression can be used to find the height, h, in. If the bottom of the ladder is sliding along the pavement directly away from the building at 2 feet/second, how fast is the top of the ladder. How high up on the building will the. The angle created by the ladder and the building is 22 degrees. The base of the ladder is 4 feet from the building. If the bottom of the ladder is sliding along the pavement directly away from the building at 3 ft/sec, how fast is the top of the ladder. A 14 foot ladder is leaning against a building. 28 square root of 2 feet b. At approximately what height does the ladder touch the building? The ladder makes a 50° angle with the ground as shown in the diagram. If the bottom of the ladder is sliding along the pavement directly away from the building at 2 feet/second, how fast is the top of the ladder. A 14 foot ladder is leaning against a building. To find out how far away the base of the ladder is from the building, we can use the pythagorean theorem. A is one leg of. Ot drawn to scale which expression can be used to find the height, h, in. Find the rate at which the area is changing at the instant the radius is 16 feet when the radius is 16 feet, the area is changing at approximately square feet per minute (round to the nearest. Trigonometric ratio is used to show the relationship between the sides and angles of a right angled triangle. This theorem applies to right triangles and states that: We want to find out how far up the building the ladder.[Solved] A 14foot ladder is leaning against a building. If the bottom
[Solved] A 14 foot ladder is leaning against a building, with the base
Solved A 14foot ladder is leaning against a building. If
Solved A 14foot ladder is leaning against a building. The angle
Solved A 14foot ladder is leaning against a building, with
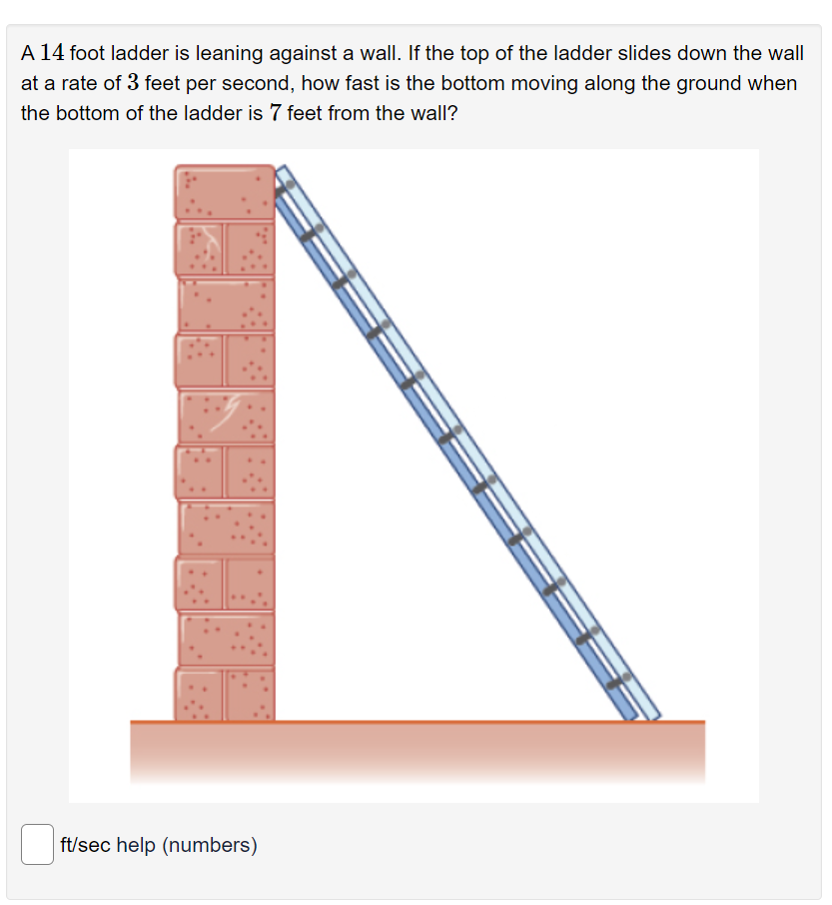
Answered A 14 ft ladder is leaning against a wall. If the top of the
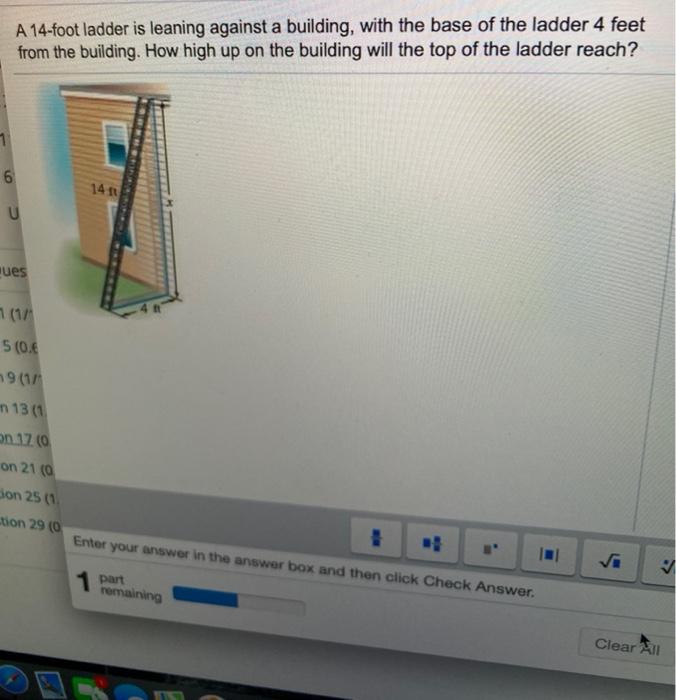
A 14foot ladder is leaning against a building, with the base of the
Solved A 14 foot ladder is leaning against a wall. If the
A 14foot ladder is leaning against a building, with the base of the
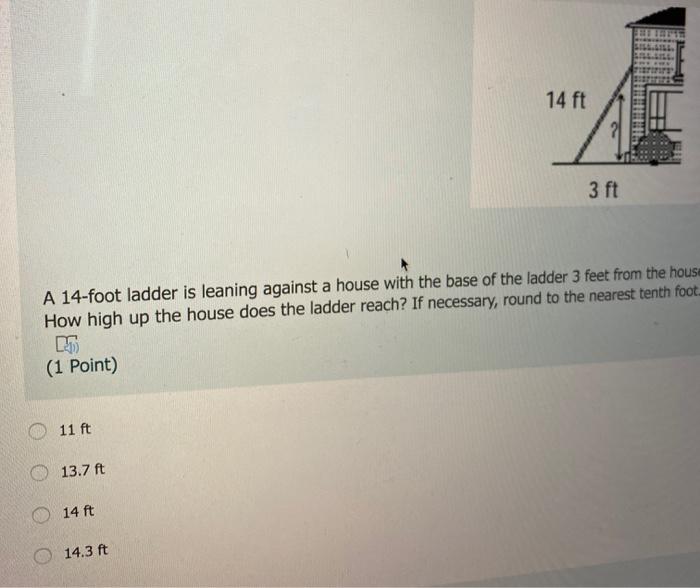
Solved 14 ft 3 ft A 14foot ladder is leaning against a
How High Up On The Building Will The Top Of The Ladder Reach?
How High Up On The Building Will The Top Of The Ladder Reach?
There Are 2 Steps To Solve This One.
How Far Up The Building Does The Ladder Reach?
Related Post: