Build Bst
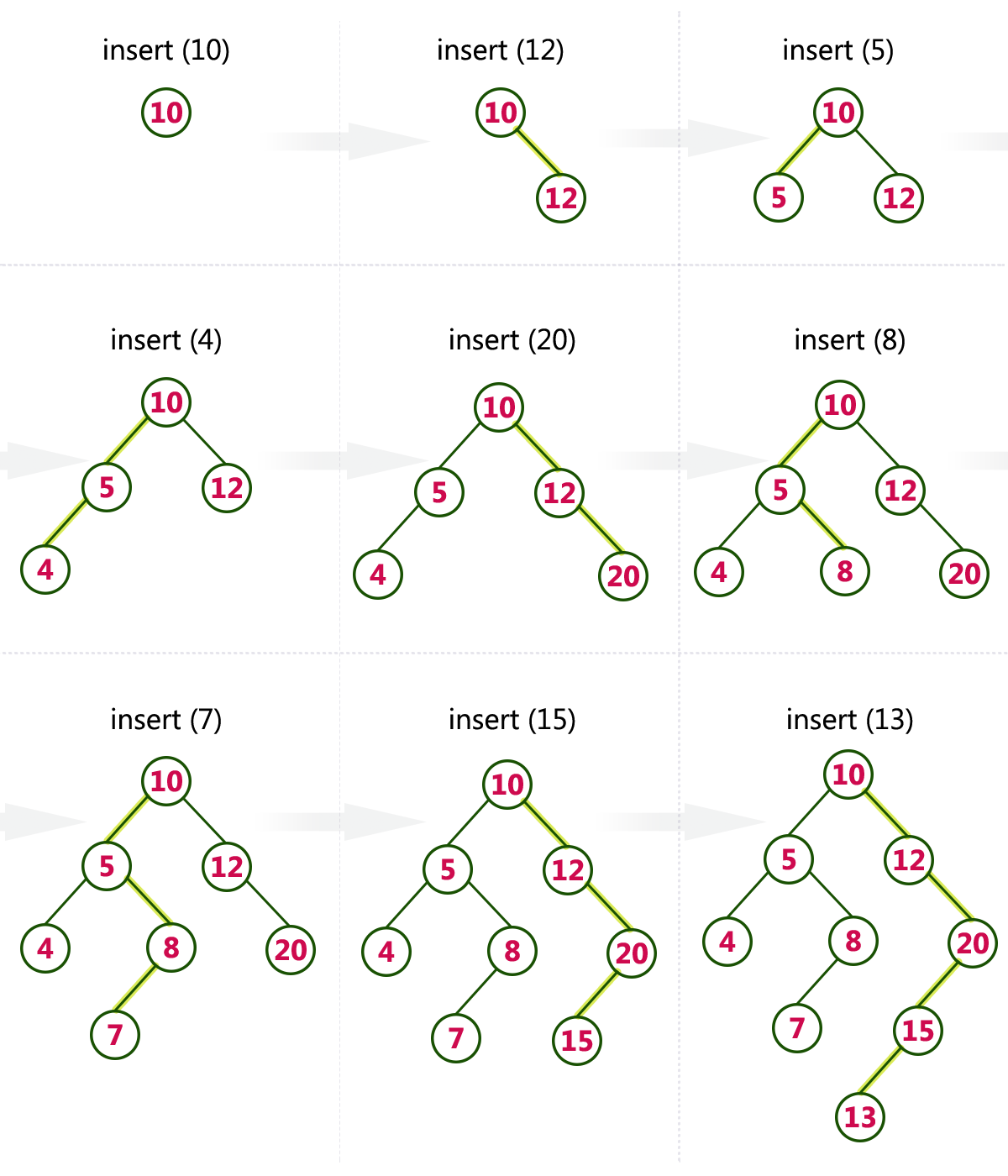
Build Bst - To create a tree you have to insert n elements in it. Finding the ceiling in a bst can be. We can easily build a bst for a given postorder sequence by recursively repeating the following steps for all keys in it, starting from the right. In a bst, it is understood that the leftmost node is the smallest node in that tree/subtree. A binary search tree (bst) is a specialized type of binary tree in which each vertex can have up to two children. By following the steps outlined above, you can create a bst that. Construct the root node of bst,. The idea is to use recursion as the first element will always be the root of the tree. Traverse through the given pre array and one by one insert every. Therefore you end up with o(n*log(n)). Therefore you end up with o(n*log(n)). We can easily build a bst for a given postorder sequence by recursively repeating the following steps for all keys in it, starting from the right. To create a tree you have to insert n elements in it. To build a balanced bst: In this article, we've explored the fascinating process of constructing a binary search tree from its given level order traversal. This structure adheres to the bst property , stipulating that every vertex in the. Find the middle element of the array, which will become the root. In a bst, it is understood that the leftmost node is the smallest node in that tree/subtree. Given the preorder traversal of a binary search tree, construct the bst. Construct the bst (binary search tree) from its given level order traversal. This structure adheres to the bst property , stipulating that every vertex in the. We can easily build a bst for a given postorder sequence by recursively repeating the following steps for all keys in it, starting from the right. Construct the root node of bst,. To create a tree you have to insert n elements in it. In this. A binary search tree (bst) is a specialized type of binary tree in which each vertex can have up to two children. Construct the root node of bst,. In a binary search tree (bst), the ceiling of a given value is the smallest element in the tree that is greater than or equal to the given value. In a bst,. Find the middle element of the array, which will become the root. To build a balanced bst: A binary search tree (bst) is a specialized type of binary tree in which each vertex can have up to two children. In a bst, it is understood that the leftmost node is the smallest node in that tree/subtree. In a binary search. This structure adheres to the bst property , stipulating that every vertex in the. In this article, we will discuss binary search. A binary search tree is a binary tree where the value of any node is greater than the left subtree and less than the right subtree. Finding the ceiling in a bst can be. Construct the bst (binary. Therefore you end up with o(n*log(n)). Given the preorder traversal of a binary search tree, construct the bst. In a binary search tree (bst), the ceiling of a given value is the smallest element in the tree that is greater than or equal to the given value. Construct the root node of bst,. Construct the bst (binary search tree) from. A binary search tree (bst) is a specialized type of binary tree in which each vertex can have up to two children. So, while currentnode’s left child is not none, we keep traversing left. A binary search tree is a binary tree where the value of any node is greater than the left subtree and less than the right subtree.. To build a balanced bst: In this article, we will discuss binary search. Construct the root node of bst,. So, while currentnode’s left child is not none, we keep traversing left. In a bst, it is understood that the leftmost node is the smallest node in that tree/subtree. A binary search tree (bst) is a specialized type of binary tree in which each vertex can have up to two children. Construct the bst (binary search tree) from its given level order traversal. In a bst, it is understood that the leftmost node is the smallest node in that tree/subtree. In this article, we've explored the fascinating process of. In a binary search tree (bst), the ceiling of a given value is the smallest element in the tree that is greater than or equal to the given value. So, while currentnode’s left child is not none, we keep traversing left. Traverse through the given pre array and one by one insert every. We can easily build a bst for. We can easily build a bst for a given postorder sequence by recursively repeating the following steps for all keys in it, starting from the right. In this article, we've explored the fascinating process of constructing a binary search tree from its given level order traversal. The idea is to use recursion as the first element will always be the. By following the steps outlined above, you can create a bst that. A binary search tree (bst) is a specialized type of binary tree in which each vertex can have up to two children. Construct the root node of bst,. We can easily build a bst for a given postorder sequence by recursively repeating the following steps for all keys in it, starting from the right. Given the preorder traversal of a binary search tree, construct the bst. In this article, we've explored the fascinating process of constructing a binary search tree from its given level order traversal. So, while currentnode’s left child is not none, we keep traversing left. Construct the bst (binary search tree) from its given level order traversal. Traverse through the given pre array and one by one insert every. To build a balanced bst: In a binary search tree (bst), the ceiling of a given value is the smallest element in the tree that is greater than or equal to the given value. Finding the ceiling in a bst can be. The idea is to use recursion as the first element will always be the root of the tree. Therefore you end up with o(n*log(n)). To insert the element in a balanced tree you need log(n). To create a tree you have to insert n elements in it.PPT ADT Binary Search Tree PowerPoint Presentation, free download
Building BSTlilgp in Visual Studio
how to create a binary search tree algorithm YouTube
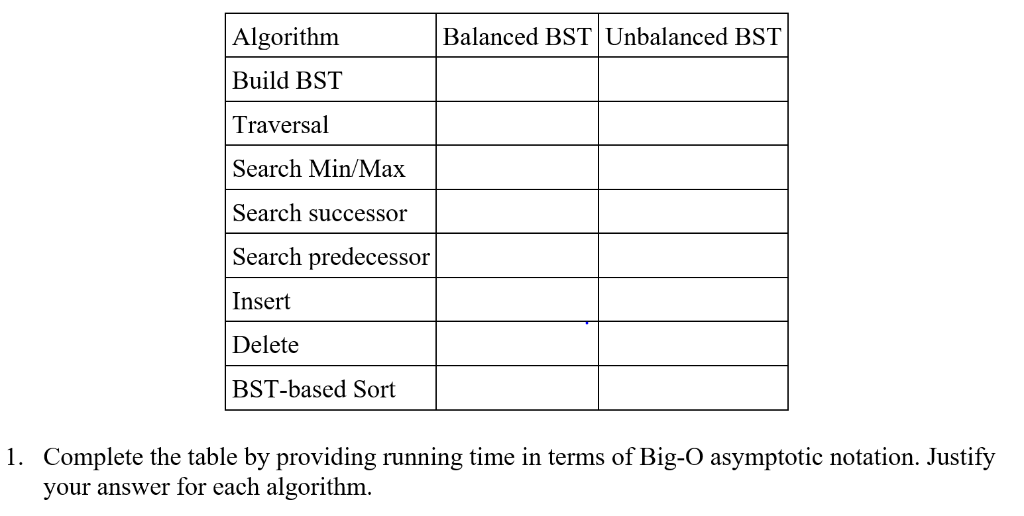
(Solved) Balanced Bst Unbalanced Bst Algorithm Build Bst Traversal
Build Balanced BST from Sorted Array C++ Placement Course Lecture
PPT ADT Binary Search Tree PowerPoint Presentation, free download
Lecture 99 Build BST from Sorted Array C++ DS Algo Placement
Build BALANCED BST Convert Normal BST to Balanced BST Ask your
Data Structures Tutorials Binary Search Tree example BST Operations
Binary Search Tree (BST) Implementation(with Full Code) Part 1
In This Article, We Will Discuss Binary Search.
Find The Middle Element Of The Array, Which Will Become The Root.
In A Bst, It Is Understood That The Leftmost Node Is The Smallest Node In That Tree/Subtree.
A Binary Search Tree Is A Binary Tree Where The Value Of Any Node Is Greater Than The Left Subtree And Less Than The Right Subtree.
Related Post: