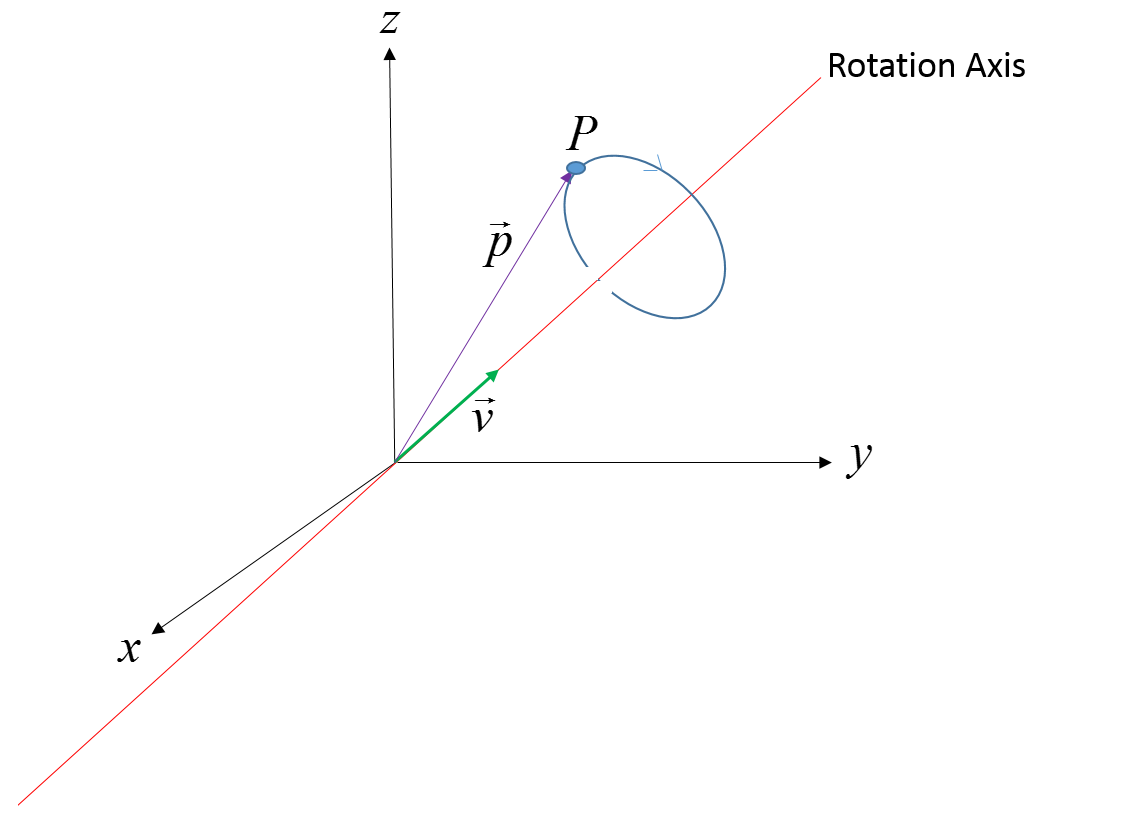
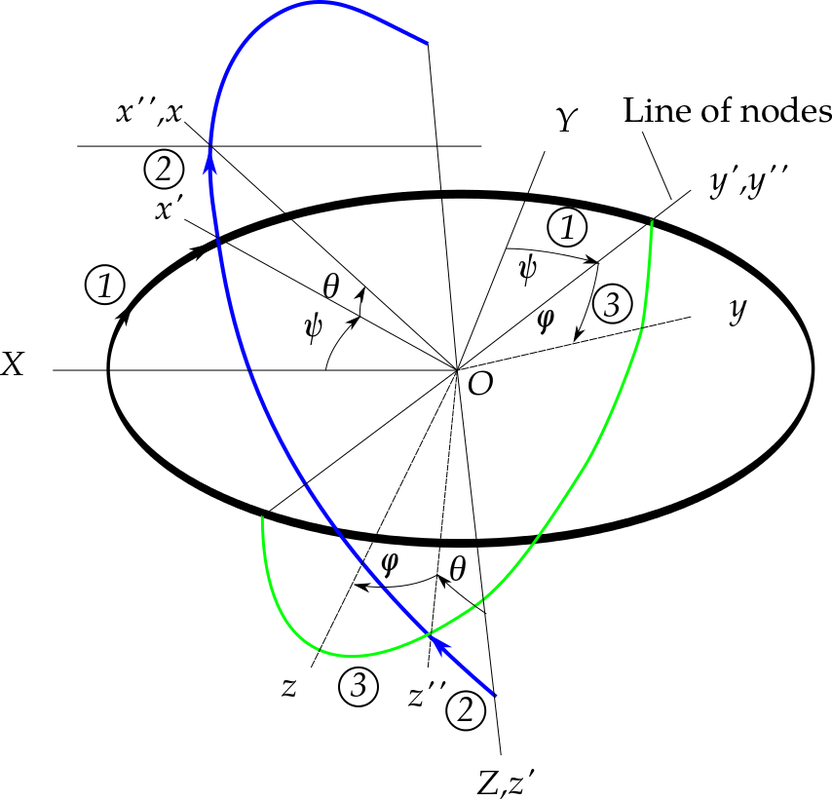
Building Rotos From Axis And Angle Quaternion

Building Rotos From Axis And Angle Quaternion - I feel like i fully understood how to convert the axis of rotation and angle to a quaternion. It is known as the swing twist decomposition: If you want to interpolate between two quaternions, do you just linearly interpolate each coordinate?. Start by finding an expression. Not to be confused with euler angles, euler integration,. Sequence of rotations (not more than three) about coordinate axes, where no two successive rotations may be about the same axis. •hamilton’s quaternions •rotation as unit quaternion •the space of rotations •photogrammetry •closed form solution of absolute orientation •division algebras, quaternion analysis, space. We give a simple definition of quaternions, and show how to convert back and forth between. Vector3 getaxis(quaternion quat) { vector3 axis = vector3(quat.x, quat.y, quat.z);. Decompose the rotation on to 2 parts.

Q = (cos(θ 2), uxsin(θ 2), uysin(θ 2), uzsin(θ 2)), i think it. We give a simple definition of quaternions, and show how to convert back and forth between. It is known as the swing twist decomposition: Not to be confused with euler angles, euler integration,. If you want to interpolate between two quaternions, do you just linearly interpolate each coordinate?. I feel like i fully understood how to convert the axis of rotation and angle to a quaternion. There is an elegant solution for this problem, specially suited for quaternions. Decompose the rotation on to 2 parts. Each choice can use static axes, or rotated axes, so we have a total of 24 euler angle versions! Representing rotations − to represent a rotation by an angle θ around an axis a = (ax, ay, az) using quaternions, we use the following unit quaternion formula − $$\mathrm{q \:=\:.

Axisangle representation of a rotation using quaternion logarithmic

Along the royal canal in dublin. Vector3 getaxis(quaternion quat) { vector3 axis = vector3(quat.x, quat.y, quat.z);. We therefore construct our desired rotation unit quaternion for a rotation by an angle $\phi$ around an axis given by unit vector $\mathbf{e}=(e_1, e_2, e_3)$ as \begin{equation} q=. This paper provides a basic introduction to the use of quaternions in 3d rotation applications. Representing.

Quaternion Rotation JCCC MATH/PHYS 191

It is known as the swing twist decomposition: Each choice can use static axes, or rotated axes, so we have a total of 24 euler angle versions! How do you calculate intermediate. •hamilton’s quaternions •rotation as unit quaternion •the space of rotations •photogrammetry •closed form solution of absolute orientation •division algebras, quaternion analysis, space. Decompose the rotation on to 2.

Axis Angle To Quaternion? The 20 Top Answers

If you want to interpolate between two quaternions, do you just linearly interpolate each coordinate?. This paper provides a basic introduction to the use of quaternions in 3d rotation applications. We therefore construct our desired rotation unit quaternion for a rotation by an angle $\phi$ around an axis given by unit vector $\mathbf{e}=(e_1, e_2, e_3)$ as \begin{equation} q=. •hamilton’s quaternions.

31+ quaternion to euler calculator AmamdaTayler

I feel like i fully understood how to convert the axis of rotation and angle to a quaternion. Decompose the rotation on to 2 parts. This paper provides a basic introduction to the use of quaternions in 3d rotation applications. How do you calculate intermediate. We therefore construct our desired rotation unit quaternion for a rotation by an angle $\phi$.

Quaternion set from axis angle method threejs demo YouTube

How do you calculate intermediate. Not to be confused with euler angles, euler integration,. Vector3 getaxis(quaternion quat) { vector3 axis = vector3(quat.x, quat.y, quat.z);. Start by finding an expression. Representing rotations − to represent a rotation by an angle θ around an axis a = (ax, ay, az) using quaternions, we use the following unit quaternion formula − $$\mathrm{q \:=\:.

theory Aerial Robotics IITK

•hamilton’s quaternions •rotation as unit quaternion •the space of rotations •photogrammetry •closed form solution of absolute orientation •division algebras, quaternion analysis, space. When all three gimbals are lined up (in the same plane), the system can only move in two. If you want to interpolate between two quaternions, do you just linearly interpolate each coordinate?. Each choice can use static.

Rotations and Quaternions Week 9, Wed 29 Oct ppt download

When defining a rotation quaternion (with vector notation) representing a rotation of θ around a vector u = (ux, uy, uz) as: Q = (cos(θ 2), uxsin(θ 2), uysin(θ 2), uzsin(θ 2)), i think it. How do you calculate intermediate. Sequence of rotations (not more than three) about coordinate axes, where no two successive rotations may be about the same.

PPT 3D Kinematics PowerPoint Presentation, free download ID4026696

Decompose the rotation on to 2 parts. Start by finding an expression. This paper provides a basic introduction to the use of quaternions in 3d rotation applications. Each choice can use static axes, or rotated axes, so we have a total of 24 euler angle versions! When defining a rotation quaternion (with vector notation) representing a rotation of θ around.

UNIVERSITY OF ILLINOIS AT URBANACHAMPAIGN ppt download

Q = (cos(θ 2), uxsin(θ 2), uysin(θ 2), uzsin(θ 2)), i think it. When defining a rotation quaternion (with vector notation) representing a rotation of θ around a vector u = (ux, uy, uz) as: Getting the axis of rotation out of a quaternion is trivial, normalize the vector component of the quaternion: It is known as the swing twist.

Axisangle representation of a rotation using quaternion logarithmic

Sequence of rotations (not more than three) about coordinate axes, where no two successive rotations may be about the same axis. Vector3 getaxis(quaternion quat) { vector3 axis = vector3(quat.x, quat.y, quat.z);. Decompose the rotation on to 2 parts. If you want to interpolate between two quaternions, do you just linearly interpolate each coordinate?. Q = (cos(θ 2), uxsin(θ 2), uysin(θ.

It Is Known As The Swing Twist Decomposition:

When all three gimbals are lined up (in the same plane), the system can only move in two. Representing rotations − to represent a rotation by an angle θ around an axis a = (ax, ay, az) using quaternions, we use the following unit quaternion formula − $$\mathrm{q \:=\:. Q = (cos(θ 2), uxsin(θ 2), uysin(θ 2), uzsin(θ 2)), i think it. We give a simple definition of quaternions, and show how to convert back and forth between.

If You Want To Interpolate Between Two Quaternions, Do You Just Linearly Interpolate Each Coordinate?.

There is an elegant solution for this problem, specially suited for quaternions. •hamilton’s quaternions •rotation as unit quaternion •the space of rotations •photogrammetry •closed form solution of absolute orientation •division algebras, quaternion analysis, space. This paper provides a basic introduction to the use of quaternions in 3d rotation applications. When defining a rotation quaternion (with vector notation) representing a rotation of θ around a vector u = (ux, uy, uz) as:

Along The Royal Canal In Dublin.

Getting the axis of rotation out of a quaternion is trivial, normalize the vector component of the quaternion: Decompose the rotation on to 2 parts. Sequence of rotations (not more than three) about coordinate axes, where no two successive rotations may be about the same axis. How do you calculate intermediate.

I Feel Like I Fully Understood How To Convert The Axis Of Rotation And Angle To A Quaternion.

We therefore construct our desired rotation unit quaternion for a rotation by an angle $\phi$ around an axis given by unit vector $\mathbf{e}=(e_1, e_2, e_3)$ as \begin{equation} q=. Vector3 getaxis(quaternion quat) { vector3 axis = vector3(quat.x, quat.y, quat.z);. Start by finding an expression. Each choice can use static axes, or rotated axes, so we have a total of 24 euler angle versions!