For All In Set Builder Notation

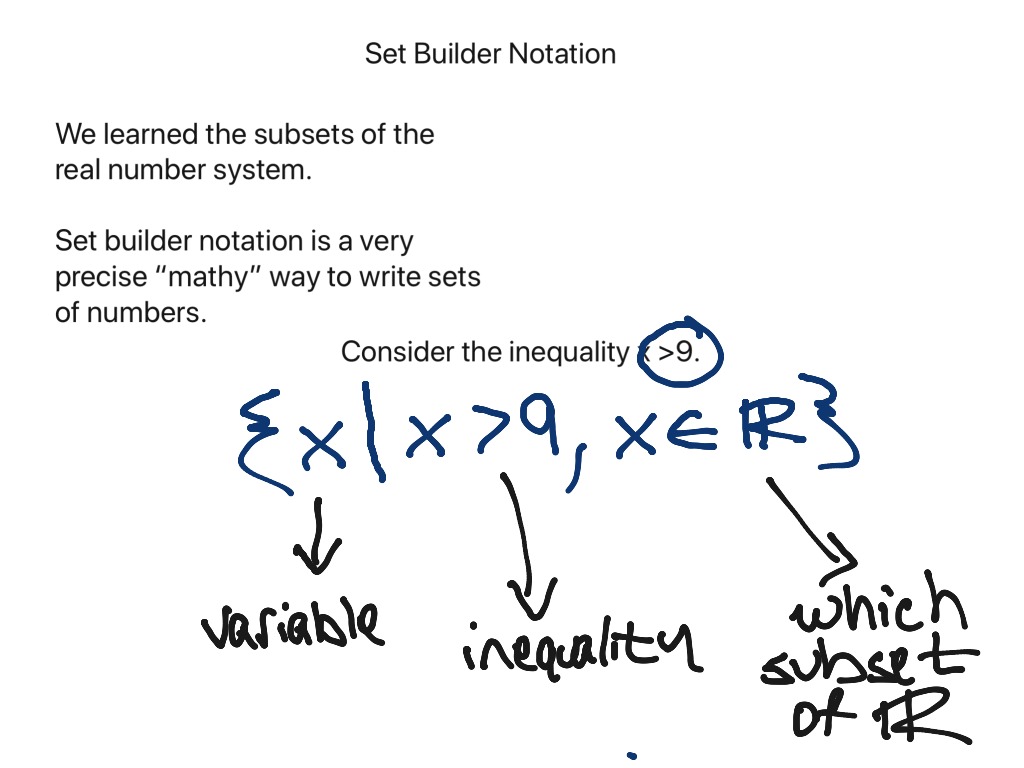
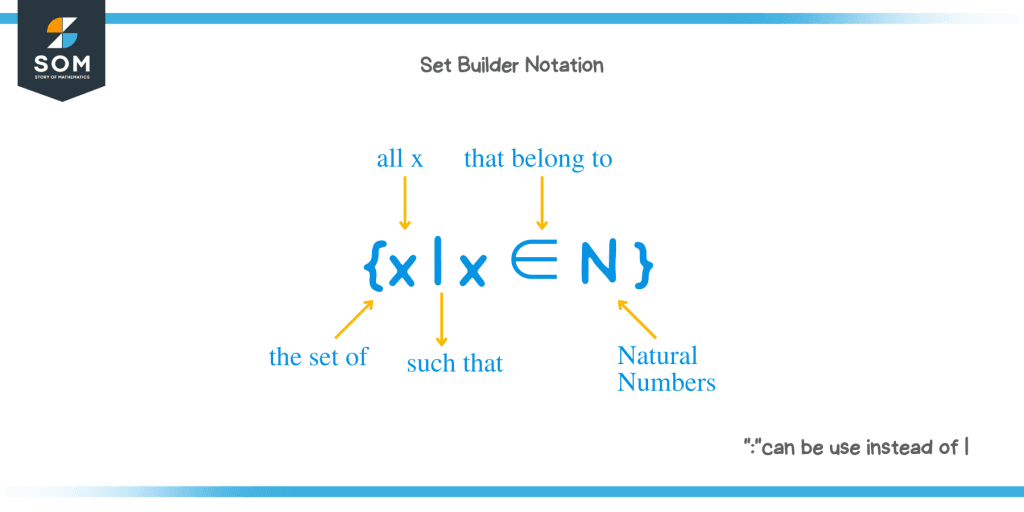
For All In Set Builder Notation - It is particularly useful when dealing with. {a | a ≤ 3} which is. It may be denoted a c or a′. Where (properties of x) is replaced by conditions that fully describe the elements of the set. More generally, we can form a subset of set a. For example, to refer to the set a a of all real numbers from 0 to 5, it is. [1] specifying sets by member properties is. For example, the set { 1, 2, 3, 4, 5, 6, 7, 8, 9 } list the elements. Both a a and b b are defined to be sets of natural numbers, so they can't be equal to s s, which contains fractions. The complement of a is the set of all elements (of u) that do not belong to a.

For example, the set { 1, 2, 3, 4, 5, 6, 7, 8, 9 } list the elements. It’s often used in mathematics to define sets in a concise way. It is particularly useful when dealing with. Based on common conventions for set builder notation, i believe the for all or any is implied. More generally, we can form a subset of set a. {a | a ≤ 3} which is. For example, to refer to the set a a of all real numbers from 0 to 5, it is. The complement may also be called the absolute. In mathematics, a set is a. Where (properties of x) is replaced by conditions that fully describe the elements of the set.

Set Builder Notation and Roster Method YouTube

More generally, we can form a subset of set a. The bar (∣) is used to separate the elements and. Based on common conventions for set builder notation, i believe the for all or any is implied. Start with all real numbers, then limit them to the interval between 2 and 6, inclusive. In mathematics, a set is a.

Set Builder Notation Cuemath

A simple example is written as. An expression, a vertical bar, and a property. Set builder notation is a way to represent sets by using the condition satisfied by every element in the set or a property followed by every element of the set or a limitation on. Normally, one writes ∃x ∈n, n = 2x ∃ x ∈ n,.

ShowMe Setbuilder notation

It may be denoted a c or a′. An important use of predicates is in set builder notation. An expression, a vertical bar, and a property. X ≥ 2 and x ≤ 6 }. We’ll often want to talk about sets that cannot be described very well by listing the elements explicitly or by taking unions,.

PPT SetBuilder Notation PowerPoint Presentation, free download ID

[1] specifying sets by member properties is. The complement of a is the set of all elements (of u) that do not belong to a. For example, the set { 1, 2, 3, 4, 5, 6, 7, 8, 9 } list the elements. A simple example is written as. The complement may also be called the absolute.

Set Builder Notation Cuemath

For example, the set { 1, 2, 3, 4, 5, 6, 7, 8, 9 } list the elements. The complement of a is the set of all elements (of u) that do not belong to a. It’s often used in mathematics to define sets in a concise way. An expression, a vertical bar, and a property. It is particularly useful.

Set Builder Notation Definition, Examples Set Builder Form

Set builder notation is a way to represent sets by using the condition satisfied by every element in the set or a property followed by every element of the set or a limitation on. In mathematics, a set is a. The complement of a is the set of all elements (of u) that do not belong to a. More generally,.

Set Builder Notation YouTube

[1] specifying sets by member properties is. An important use of predicates is in set builder notation. A simple example is written as. Set builder notation is a way to represent sets by using the condition satisfied by every element in the set or a property followed by every element of the set or a limitation on. The bar (∣).

Set builder notation Explanation and Examples

X ≥ 2 and x ≤ 6 }. Where (properties of x) is replaced by conditions that fully describe the elements of the set. It may be denoted a c or a′. Start with all real numbers, then limit them to the interval between 2 and 6, inclusive. Both a a and b b are defined to be sets of.

Set Builder Notation Cuemath

The bar (∣) is used to separate the elements and. Set builder notation is a way to represent sets by using the condition satisfied by every element in the set or a property followed by every element of the set or a limitation on. The complement of a is the set of all elements (of u) that do not belong.

SetBuilder Notation for Algebraic Numbers

For example, the set { 1, 2, 3, 4, 5, 6, 7, 8, 9 } list the elements. An important use of predicates is in set builder notation. {a | a ≤ 3} which is. Both a a and b b are defined to be sets of natural numbers, so they can't be equal to s s, which contains fractions..

The Bar (∣) Is Used To Separate The Elements And.

X ≥ 2 and x ≤ 6 }. In mathematics, a set is a. It may be denoted a c or a′. [1] specifying sets by member properties is.

Based On Common Conventions For Set Builder Notation, I Believe The For All Or Any Is Implied.

It is particularly useful when dealing with. Where (properties of x) is replaced by conditions that fully describe the elements of the set. Normally, one writes ∃x ∈n, n = 2x ∃ x ∈ n, n = 2 x, there. Start with all real numbers, then limit them to the interval between 2 and 6, inclusive.

The Complement May Also Be Called The Absolute.

Set builder notation is a way to represent sets by using the condition satisfied by every element in the set or a property followed by every element of the set or a limitation on. An expression, a vertical bar, and a property. {a | a ≤ 3} which is. A simple example is written as.

An Important Use Of Predicates Is In Set Builder Notation.

For example, the set { 1, 2, 3, 4, 5, 6, 7, 8, 9 } list the elements. More generally, we can form a subset of set a. The complement of a is the set of all elements (of u) that do not belong to a. It’s often used in mathematics to define sets in a concise way.