How To Build A Binary Search Tree
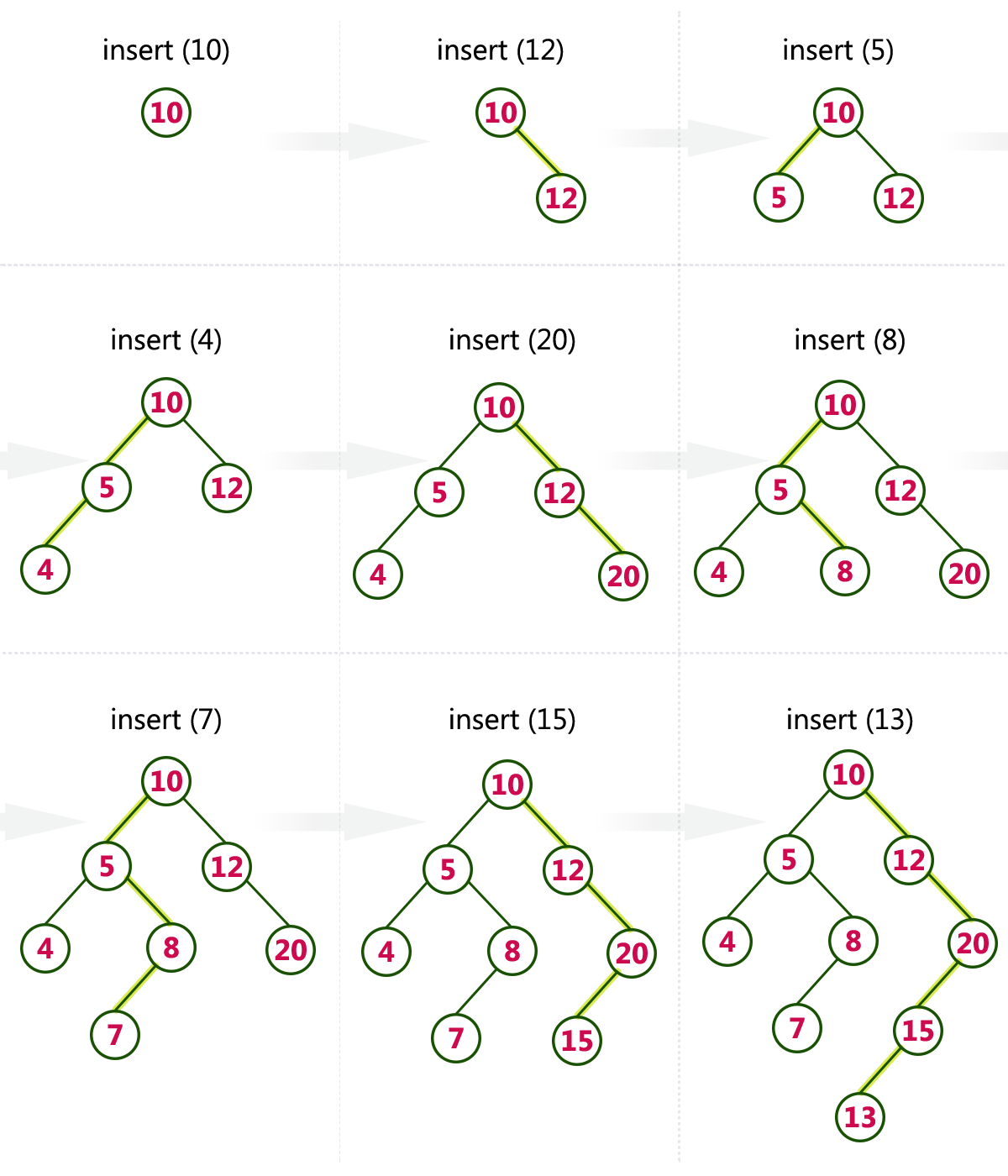
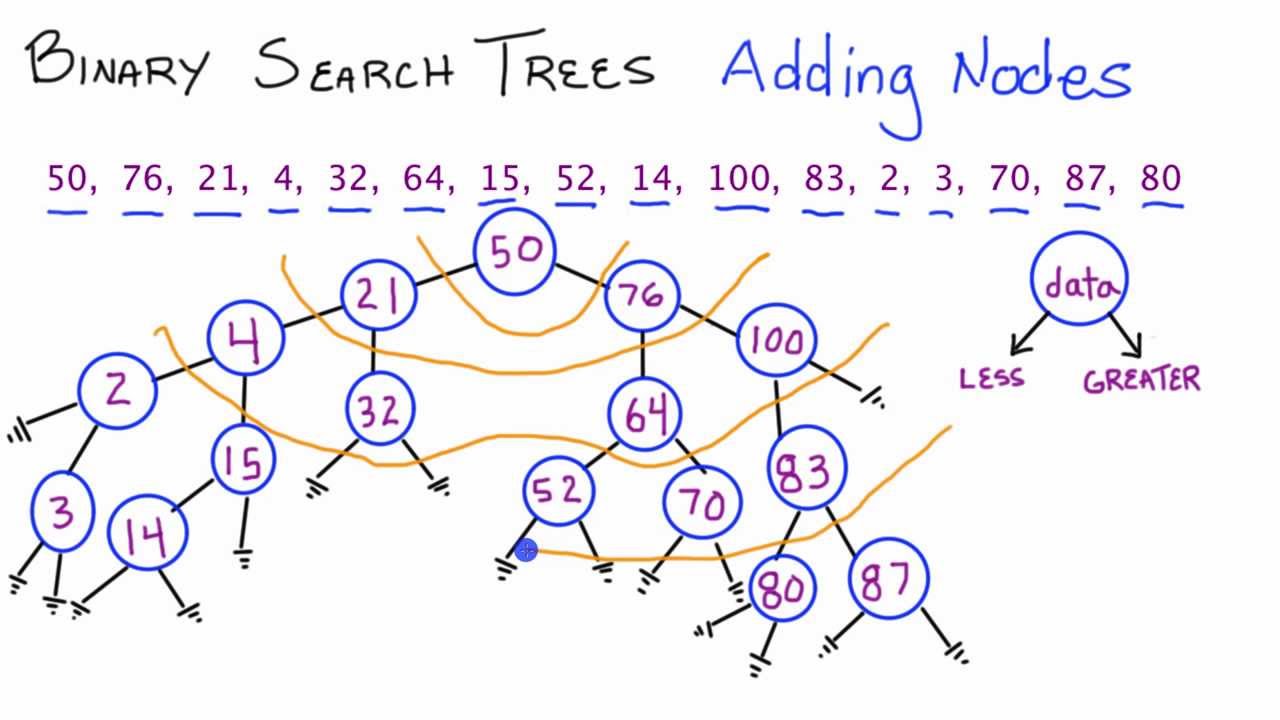
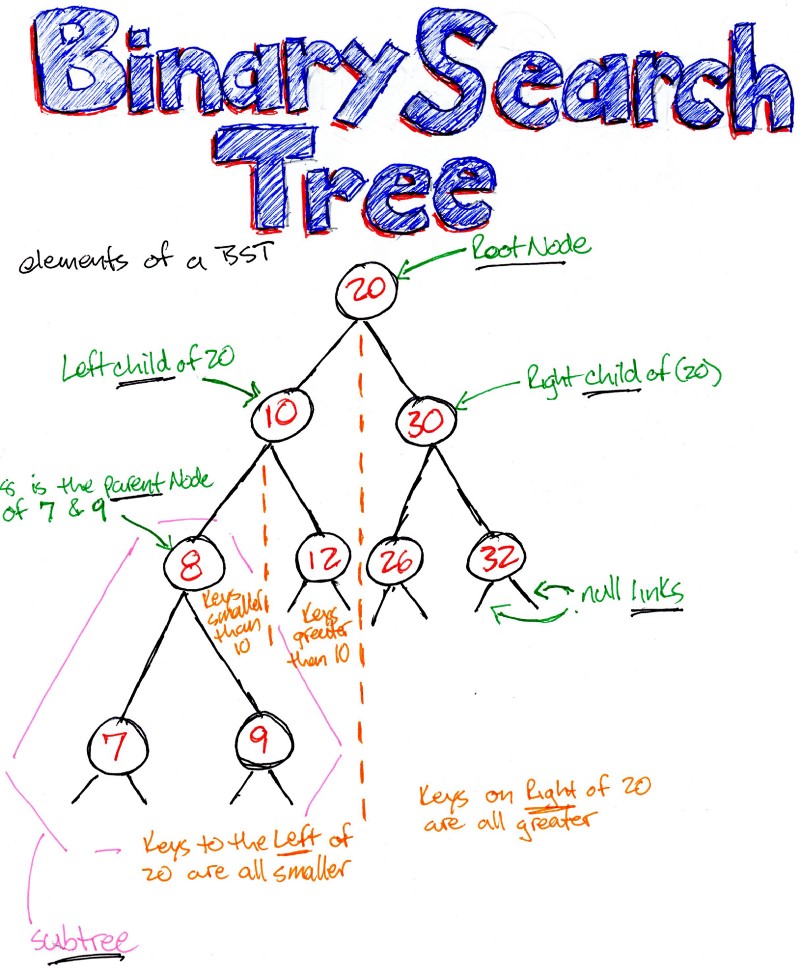
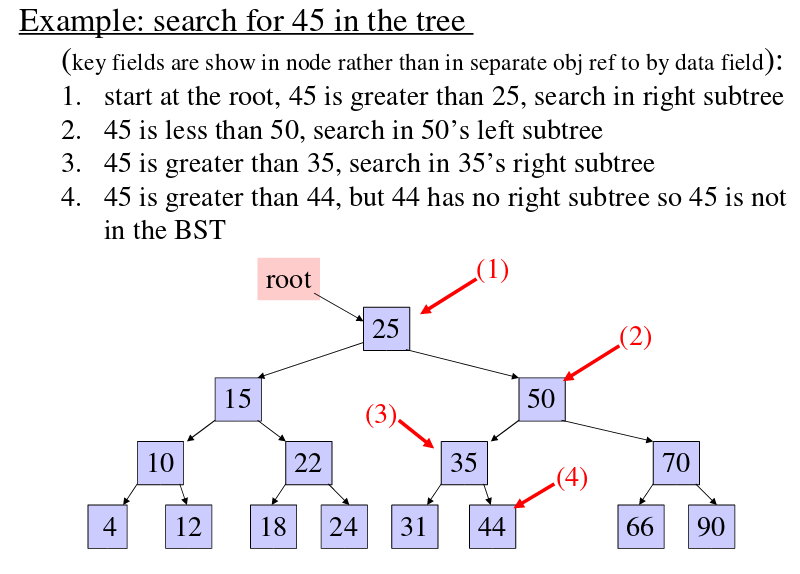
How To Build A Binary Search Tree - In this article, we will discuss binary search. Now we can easily perform search operation in bst using. Well, binary search trees or bst are a special variant of trees that come with a very unique condition for filling in the left and right children of every node in the tree. If the target is greater than the middle element, search the right half. Given a bst, the task is to search a node in this bst. (there are algorithms which try to minimise. A binary search tree is a binary tree data structure with the following properties. We know that for an array, we can use binary search to find an element faster. A binary search tree is a binary tree where the value of any node is greater than the left subtree and less than the right subtree. It allows search, insert, delete, ceiling,. In this tutorial, you will learn what a binary search tree is, what parts make up a tree, and some of the common terms we use when describing parts of a tree. A parent node has, at most, 2 child nodes. For a short explanation of binary search, check out this link. This rule is applied recursively to the left. We can implement a binary tree node in python as follows. Let’s begin by first establishing some rules for binary search trees: Yet, correlates of the likelihood to use. A binary search tree is a binary tree where the value of any node is greater than the left subtree and less than the right subtree. (there are algorithms which try to minimise. If the target is less than the middle element, search the left half. This rule is applied recursively to the left. In this article, we will discuss binary search. Specifically, in log n \log n lo g n time. In a binary search tree, the value of left node must be smaller than the parent node, and the value of right node must be greater than the parent node. The right child. The right child node is. In this article, we will discuss binary search. Refer the one on the left. In a binary search tree, the value of left node must be smaller than the parent node, and the value of right node must be greater than the parent node. Let’s begin by first establishing some rules for binary search trees: The left child node is always less than the parent node. In a binary search tree, the value of left node must be smaller than the parent node, and the value of right node must be greater than the parent node. From this point on, we will refer a vertex in a binary tree as a node and put the. If the target is less than the middle element, search the left half. Deletes a node from the tree. In this tutorial, you will learn what a binary search tree is, what parts make up a tree, and some of the common terms we use when describing parts of a tree. Specifically, in log n \log n lo g. We know that for an array, we can use binary search to find an element faster. The right child node is. Given a bst, the task is to search a node in this bst. If the target is less than the middle element, search the left half. Searches for a node in the tree. Deletes a node from the tree. If the target is greater than the middle element, search the right half. Refer the one on the left. If the target is less than the middle element, search the left half. Insert a node in the tree. In this tutorial, you will learn what a binary search tree is, what parts make up a tree, and some of the common terms we use when describing parts of a tree. Given a binary tree, find out if it is binary search tree or not. For searching a value in bst, consider it as a sorted array. Now we. In this tutorial, you will learn what a binary search tree is, what parts make up a tree, and some of the common terms we use when describing parts of a tree. Now we can easily perform search operation in bst using. If the target is greater than the middle element, search the right half. In this article, we will. For a short explanation of binary search, check out this link. If the target is less than the middle element, search the left half. This rule is applied recursively to the left. Let’s begin by first establishing some rules for binary search trees: Searches for a node in the tree. For searching a value in bst, consider it as a sorted array. In this tutorial, you will learn what a binary search tree is, what parts make up a tree, and some of the common terms we use when describing parts of a tree. The left child node is always less than the parent node. Insert a node in the. It allows search, insert, delete, ceiling,. In this article, we will discuss binary search. Deletes a node from the tree. In a binary search tree, the value of left node must be smaller than the parent node, and the value of right node must be greater than the parent node. A binary search tree is useful for maintaining sorted stream of data. In this tutorial, you will learn what a binary search tree is, what parts make up a tree, and some of the common terms we use when describing parts of a tree. Specifically, in log n \log n lo g n time. This rule is applied recursively to the left. Yet, correlates of the likelihood to use. For a short explanation of binary search, check out this link. We know that for an array, we can use binary search to find an element faster. What is a binary search tree? Given a binary tree, find out if it is binary search tree or not. (there are algorithms which try to minimise. From this point on, we will refer a vertex in a binary tree as a node and put the children below their parent with one on the left and one on the right. Searches for a node in the tree.Data Structures Tutorials Binary Search Tree example BST Operations
how to create a binary search tree algorithm YouTube
Binary Search Trees Adding Nodes Part 1 C++ How to Add Nodes to
Binary Search Tree (BST) Implementation(with Full Code) Part 1
How to Create a Binary Search Tree from an Array
Data Structures 101 Binary Search Tree
110. Create Binary Search Tree (Hindi) YouTube
How to Construct a Binary Search Tree YouTube
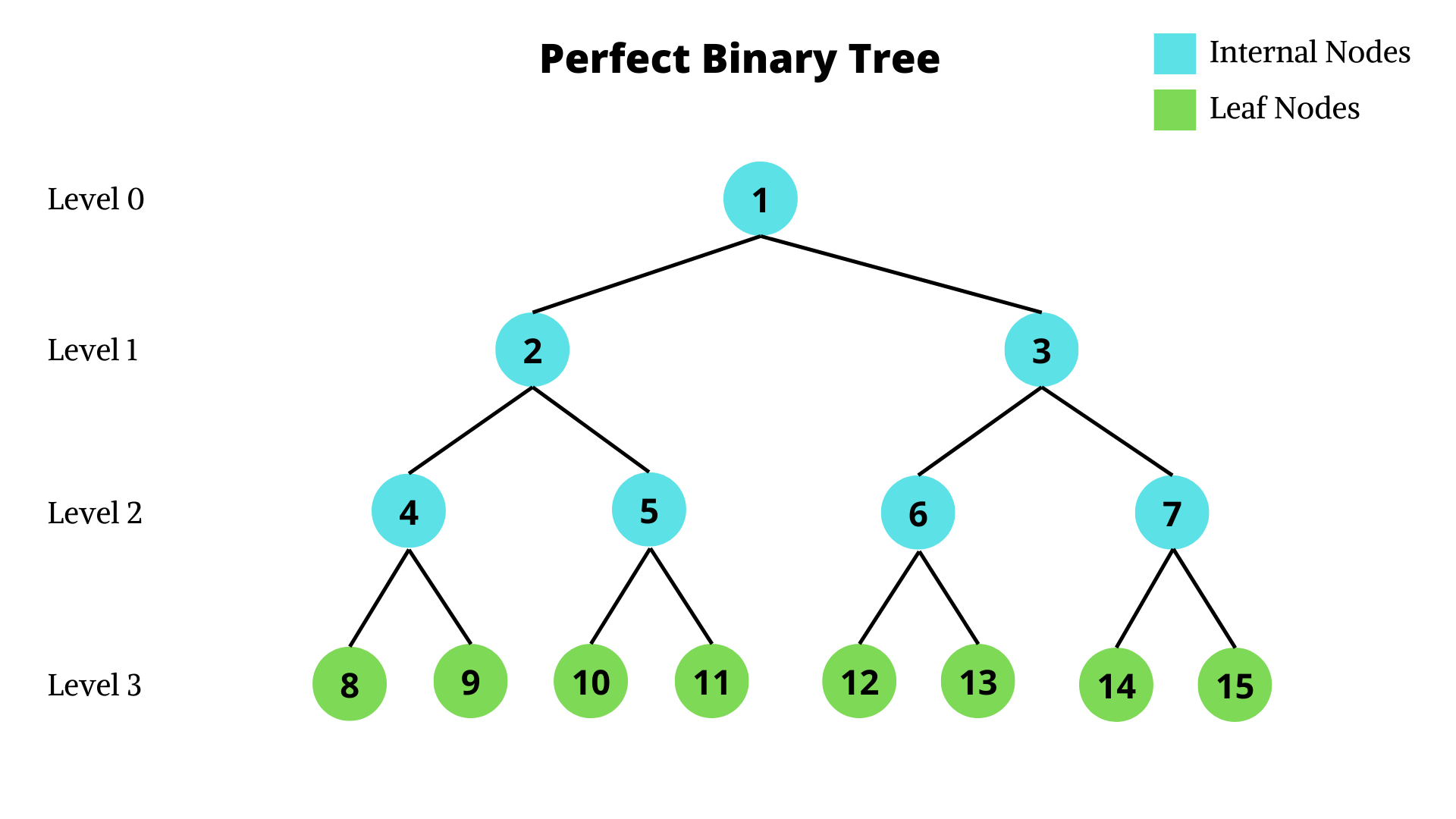
Perfect Binary Tree
Binary Search Tree Set 1 (Search and Insertion)
Insert A Node In The Tree.
The Left Child Node Is Always Less Than The Parent Node.
According To Your Logic, Second One Is The Correct Way.
If The Target Is Less Than The Middle Element, Search The Left Half.
Related Post: