Inequality In Set Builder Notation

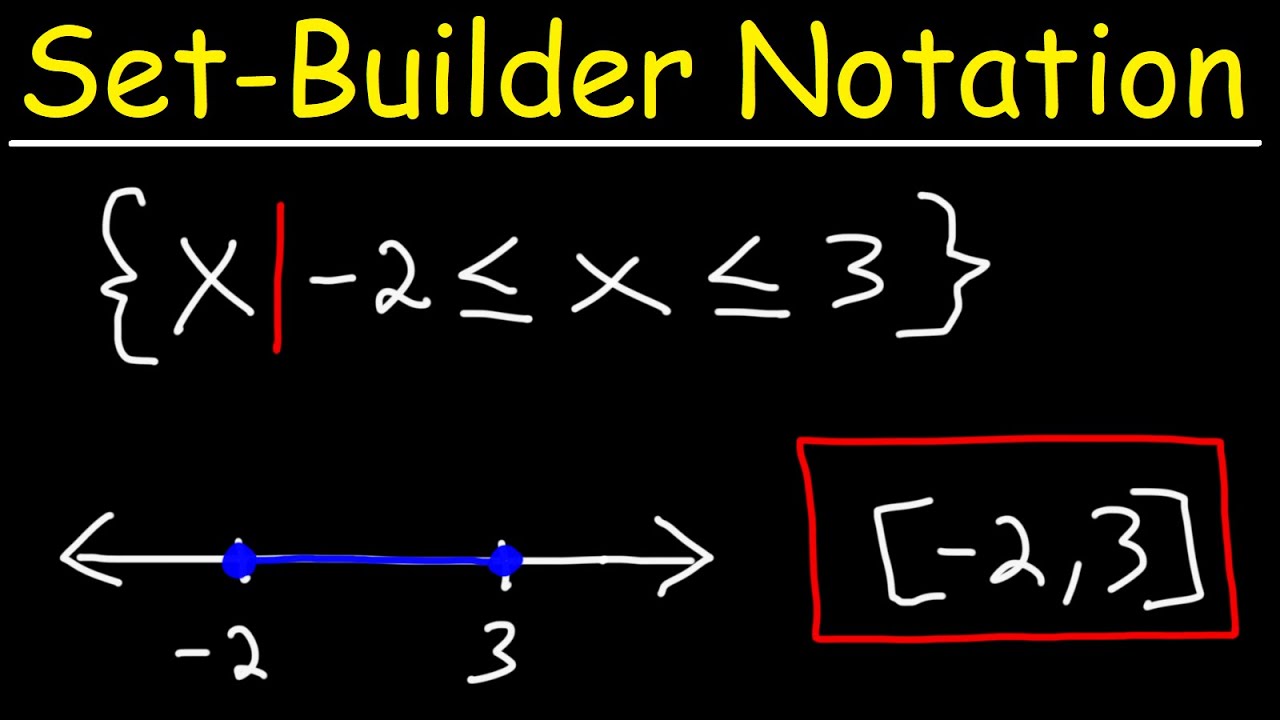
Inequality In Set Builder Notation - They are also used in the definitions of limits and with derivatives to study where functions are increasing. We will use two types of notation to write the solution set of an inequality: When multiplying or dividing both sides of an inequality by a negative number, flip the inequality symbol! Let's look at a few examples that deal with interval notation,. Interval notation uses parentheses, ( ), and brackets, [ ]. There are two notations for writing inequalities besides the basic style. An important use of predicates is in set builder notation. In this lesson, we will discuss ranges on a number line and how we can express these ranges using either interval notation or set builder notation. Solve inequalities just like how we solve equations. * x 5 * y = 5

There are two notations for writing inequalities besides the basic style. With this convention, sets are built with. Let's look at a few examples that deal with interval notation,. We will use two types of notation to write the solution set of an inequality: Need some extra practice converting solution phrases into set builder notation? In this lesson, we will discuss ranges on a number line and how we can express these ranges using either interval notation or set builder notation. 2 − 5 < 3 +5 + 5. Interval notation uses parentheses, ( ), and brackets, [ ]. Another commonly used, and arguably the most concise, method for describing inequalities and solutions to inequalities is called interval notation. We’ll often want to talk about sets that cannot be described very well by listing the elements explicitly or by taking unions,.

Domain and Range Algebra and Trigonometry

Set builder notation is the descriptive definition of the set. Another commonly used, and arguably the most concise, method for describing inequalities and solutions to inequalities is called interval notation. With this convention, sets are built with. Solve inequalities just like how we solve equations. Let's look at a few examples that deal with interval notation,.

Solve the inequality and write the solution in setbuilder notation. r 8

An important use of predicates is in set builder notation. We will be introduced to linear inequalities,. Usually, you'll see it when you learn about solving inequalities, because for some reason saying x < 3 isn't good enough, so instead they'll want you to phrase the answer as the solution set. In this lesson, we will discuss ranges on a.

Domain and Range. ppt download

Set builder notation is the descriptive definition of the set. 2 − 5 < 3 +5 + 5. Inequalities are needed to study where functions have positive and negative values. Let's look at a few examples that deal with interval notation,. Share an example of a set described using both systems.

Interval Notation to SetBuilder Notation PreCalculus YouTube

An important use of predicates is in set builder notation. How do you write inequalities in set builder notation? Usually, you'll see it when you learn about solving inequalities, because for some reason saying x < 3 isn't good enough, so instead they'll want you to phrase the answer as the solution set. {x | x > 14} basically, this.

Solve the given inequality. Describe the solution set using the set

Set builder notation is the descriptive definition of the set. Solve inequalities just like how we solve equations. In this lesson, we will discuss ranges on a number line and how we can express these ranges using either interval notation or set builder notation. {x | x > 14} basically, this is just saying that x is any real number.

Compound Inequalities, And, Or. Solve, Graph, Write in Interval

We will be introduced to linear inequalities,. Need some extra practice converting solution phrases into set builder notation? We’ll often want to talk about sets that cannot be described very well by listing the elements explicitly or by taking unions,. With this convention, sets are built with. Let's look at a few examples that deal with interval notation,.

ShowMe Setbuilder notation inequality

With this convention, sets are built with. Interval notation uses parentheses, ( ), and brackets, [ ]. How do you write inequalities in set builder notation? Share an example of a set described using both systems. Set builder notation is the descriptive definition of the set.

Connecting Inequality Notation, Interval Notation, SetBuilder Notation

Interval notation uses parentheses, ( ), and brackets, [ ]. We will use two types of notation to write the solution set of an inequality: Share an example of a set described using both systems. Need some extra practice converting solution phrases into set builder notation? Explain why we do not use a bracket in interval notation when.

Solve the inequality and write the solution in setbuilder notation. r 8

Another commonly used, and arguably the most concise, method for describing inequalities and solutions to inequalities is called interval notation. Another commonly used, and arguably the most concise, method for describing inequalities and solutions to inequalities is called interval notation. They are also used in the definitions of limits and with derivatives to study where functions are increasing. We use.

Introduction to Inequalities and Interval Notation

Set builder notation is the descriptive definition of the set. Let's look at a few examples that deal with interval notation,. Write the following in set builder notation. {x | x > 14} basically, this is just saying that x is any real number that is larger than 14. Usually, you'll see it when you learn about solving inequalities, because.

We Will Be Introduced To Linear Inequalities,.

When we have inequalities that involve variables, there is often an infinite number of values the variable can take. Usually, you'll see it when you learn about solving inequalities, because for some reason saying x < 3 isn't good enough, so instead they'll want you to phrase the answer as the solution set. Interval notation uses parentheses, ( ), and brackets, [ ]. Write the following in set builder notation.

Another Commonly Used, And Arguably The Most Concise, Method For Describing Inequalities And Solutions To Inequalities Is Called Interval Notation.

Solve inequalities just like how we solve equations. An important use of predicates is in set builder notation. Another commonly used, and arguably the most concise, method for describing inequalities and solutions to inequalities is called interval notation. When multiplying or dividing both sides of an inequality by a negative number, flip the inequality symbol!

With This Convention, Sets Are Built With.

How do you write inequalities in set builder notation? There are two notations for writing inequalities besides the basic style. For example, figure skaters and gymnasts frequently want to know. In this lesson, we will discuss ranges on a number line and how we can express these ranges using either interval notation or set builder notation.

Explain Why We Do Not Use A Bracket In Interval Notation When.

{x | x > 14} basically, this is just saying that x is any real number that is larger than 14. We will use two types of notation to write the solution set of an inequality: Let's look at a few examples that deal with interval notation,. We’ll often want to talk about sets that cannot be described very well by listing the elements explicitly or by taking unions,.