Set Builder Notation All Real Numbers
Set Builder Notation All Real Numbers - The same set could be. Second, if there is a denominator in the function’s equation,. There are two common ways to describe a set of real numbers that satisfy certain conditions: Set builder notation can be written in two ways. X ≥ 2 and x ≤ 6 } The set of all real numbers between 0 and 1 is not countably infinite countably infinite finite, because any infinite sequence of real numbers will necessarily fail to include all real numbers. In mathematics, set builder notation is a mathematical notation of describing a set by listing its elements or demonstrating its properties that its members must satisfy. $$\{\text{what elements of the set look like} \mid \text{what needs to be true of those elements}\}$$ where the. Start with all real numbers, then limit them to the interval between 2 and 6, inclusive. We can state a function’s domain as “all real numbers” if its domain is exclusively made up of real. Set builder notation can be written in two ways. But the shortened version of set builder. A shorthand used to write sets, often sets with an infinite number of elements. For example, the set { 1, 2, 3, 4, 5, 6, 7, 8, 9 } list the elements. X ≥ 2 and x ≤ 6 } In set builder notation, the domain of f(x) = 1/x may be written as {x ∈ ℝ | x ≠ 0}. An important use of predicates is in set builder notation. One uses braces { } and the other does not. An expression, a vertical bar, and a property. X ∈ r, x > 2 and x < 10 }. Set builder notation can be written in two ways. An expression, a vertical bar, and a property. In algebra courses we usually use interval notation. A shorthand used to write sets, often sets with an infinite number of elements. But the shortened version of set builder. First, if the function has no denominator or an even root, consider whether the domain could be all real numbers. We’ll often want to talk about sets that cannot be described very well by listing the elements explicitly or by taking. In algebra courses we usually use interval notation. A shorthand used to write sets, often sets with an infinite. Second, if there is a denominator in the function’s equation,. For example, the set { 1, 2, 3, 4, 5, 6, 7, 8, 9 } list the elements. Start with all real numbers, then limit them to the interval between 2 and 6, inclusive. X ∈ r, x > 2 and x < 10 }. In mathematics, a set is. For example, the set { 1, 2, 3, 4, 5, 6, 7, 8, 9 } list the elements. In mathematics, set builder notation is a mathematical notation of describing a set by listing its elements or demonstrating its properties that its members must satisfy. We can represent the set of all real numbers between 2 and 10 as follows using. X ∈ r, x > 2 and x < 10 }. $$\{\text{what elements of the set look like} \mid \text{what needs to be true of those elements}\}$$ where the. An important use of predicates is in set builder notation. A shorthand used to write sets, often sets with an infinite number of elements. We’ll often want to talk about sets. Set builder notation can be written in two ways. {x \in r | x x∈r∣x > 0} should be read as the set of all x's that are an element of the real numbers such that x is greater than 0. special symbols: The same set could be. An important use of predicates is in set builder notation. Start with. There are two common ways to describe a set of real numbers that satisfy certain conditions: We can state a function’s domain as “all real numbers” if its domain is exclusively made up of real. X > 0} is read aloud, the set of all x such that x is greater than 0. it is read aloud exactly the. X. But the shortened version of set builder. First, if the function has no denominator or an even root, consider whether the domain could be all real numbers. This notation is read as “the set of all x such that x is an element of the real numbers,. An important use of predicates is in set builder notation. Start with all. X ∈ r, x > 2 and x < 10 }. X ≥ 2 and x ≤ 6 } One uses braces { } and the other does not. Second, if there is a denominator in the function’s equation,. $$\{\text{what elements of the set look like} \mid \text{what needs to be true of those elements}\}$$ where the. An expression, a vertical bar, and a property. A shorthand used to write sets, often sets with an infinite number of elements. Second, if there is a denominator in the function’s equation,. This notation is read as “the set of all x such that x is an element of the real numbers,. X ≥ 2 and x ≤ 6 } A set of polygons in an euler diagram this set equals the one depicted above since both have the very same elements. X > 0} is read aloud, the set of all x such that x is greater than 0. it is read aloud exactly the. There are two common ways to describe a set of real numbers that satisfy certain conditions: In mathematics, set builder notation is a mathematical notation of describing a set by listing its elements or demonstrating its properties that its members must satisfy. Set builder notation can be written in two ways. But the shortened version of set builder. {x \in r | x x∈r∣x > 0} should be read as the set of all x's that are an element of the real numbers such that x is greater than 0. special symbols: The set of all real numbers between 0 and 1 is not countably infinite countably infinite finite, because any infinite sequence of real numbers will necessarily fail to include all real numbers. We can represent the set of all real numbers between 2 and 10 as follows using the set builder notation: In algebra courses we usually use interval notation. For example, the set { 1, 2, 3, 4, 5, 6, 7, 8, 9 } list the elements.2_Set_Builder_Notation_and_Sets_of_Real_Numbers Notes
Set Builder Notation and Roster Method YouTube
Solved Use set builder notation to describe the set of all
SetBuilder Notation for Algebraic Numbers
Set Builder Notation Cuemath
Setbuilder and interval notations for describing sets of real numbers
Set Builder Notation Definition, Examples Set Builder Form
2_Set_Builder_Notation_and_Sets_of_Real_Numbers
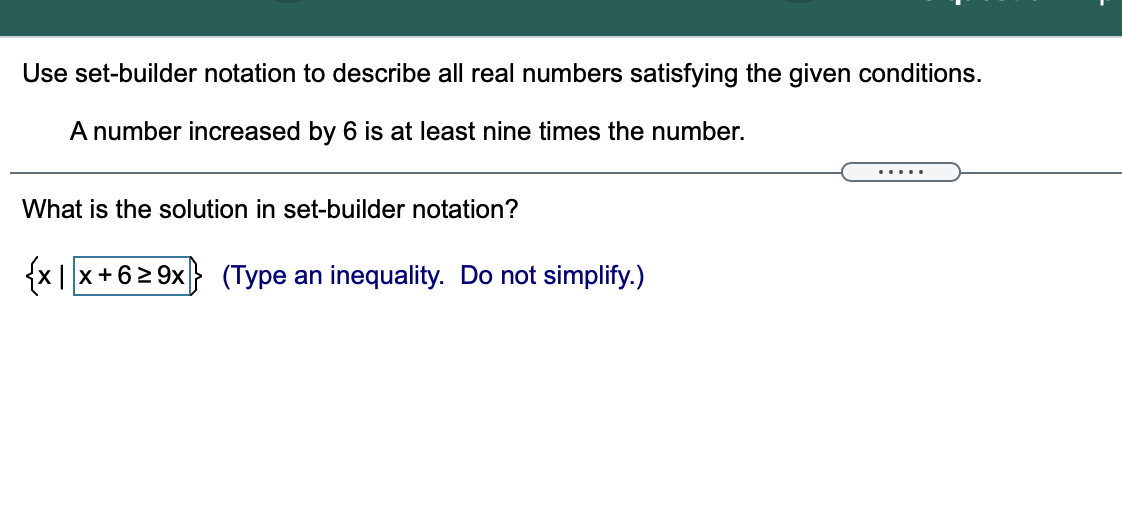
Solved Use setbuilder notation to describe all real numbers
An Important Use Of Predicates Is In Set Builder Notation.
The Same Set Could Be.
We Can State A Function’s Domain As “All Real Numbers” If Its Domain Is Exclusively Made Up Of Real.
In Mathematics, A Set Is A Collection Of Different [1] Things;
Related Post: