Set Builder Notation Math Stack

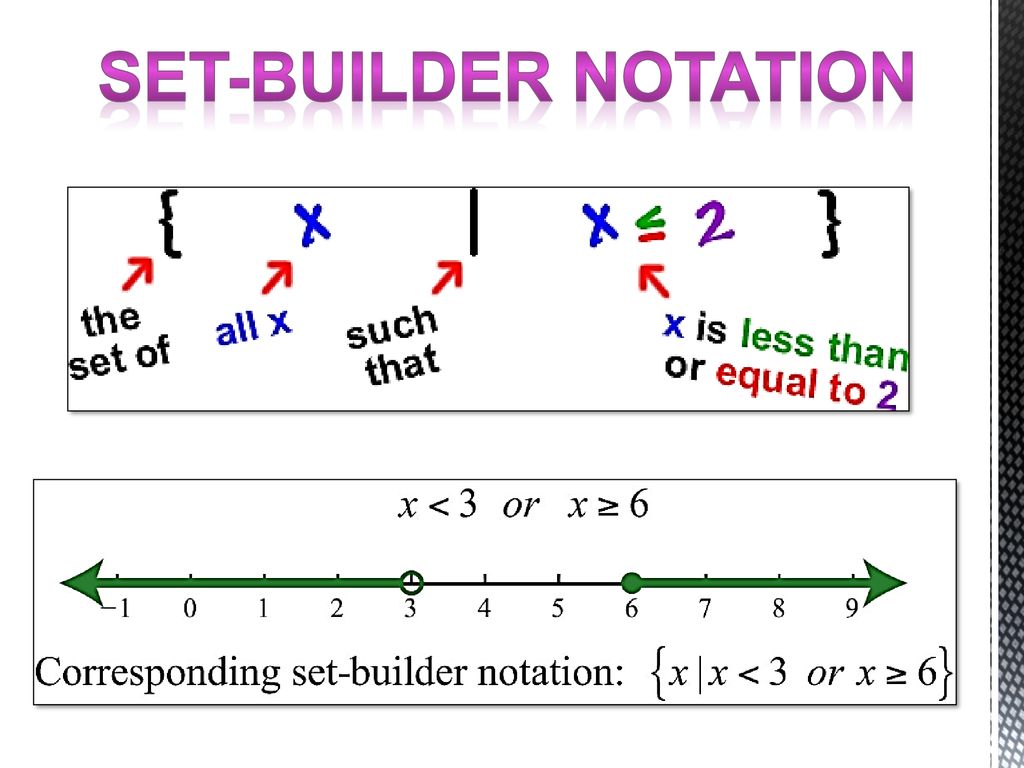
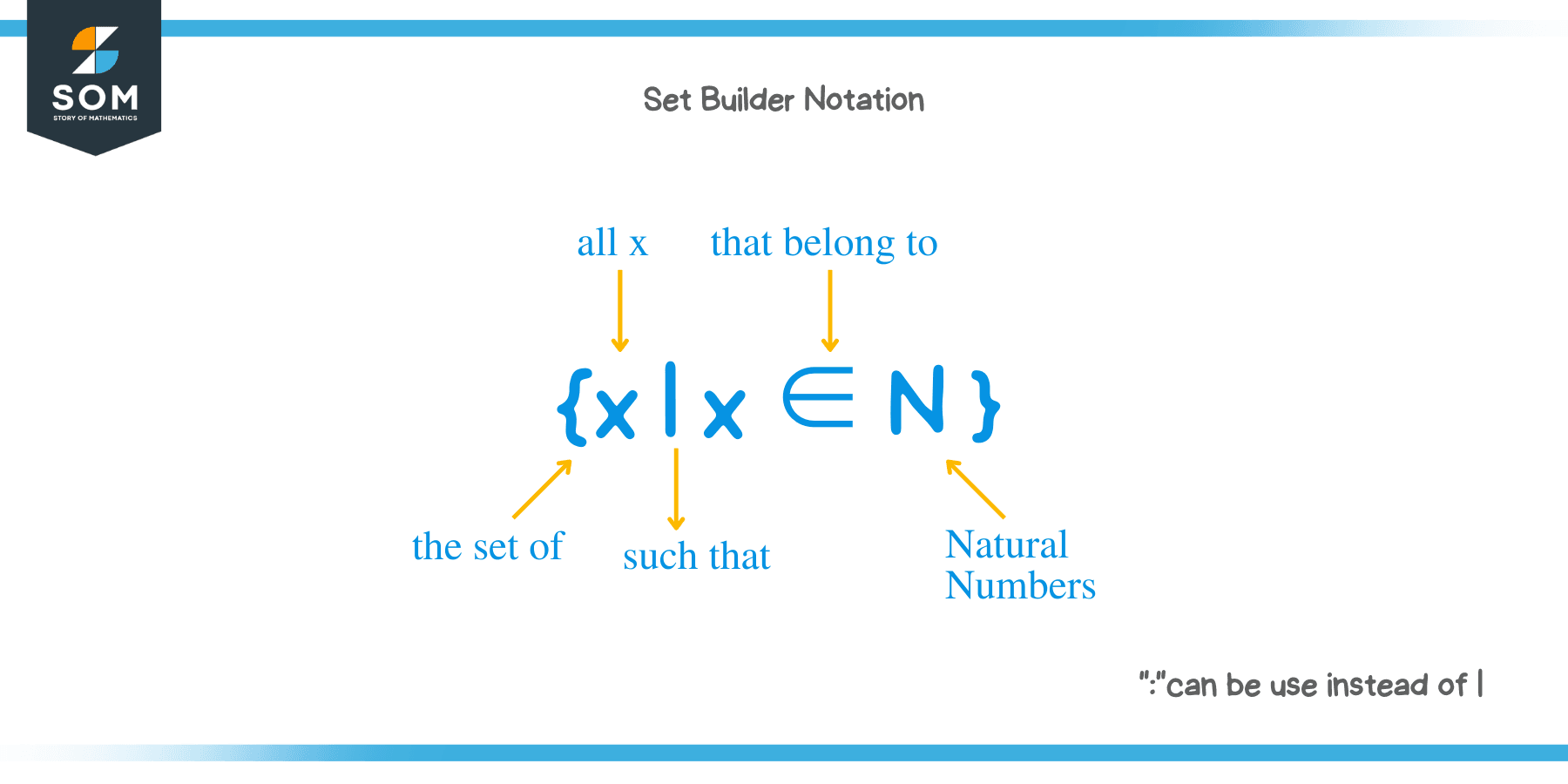
Set Builder Notation Math Stack - Definition 1.let a and b be sets. Defenition of a set (8:41) number sets. \}$ is a useful way to represent a set which is characterized by some rule or property, nothing more. It does not evaluate to a true/false condition which tells us in which case. [1] specifying sets by member properties is. Master discrete math, the backbone of mathematics and computer science. In some treatments of the subject. P(x)\}$ is equal to $\{y : An important use of predicates is in set builder notation. Someone use : instead of |.

Describe the set of all odd numbers between $100$ and $200$ using set builder notation Master discrete math, the backbone of mathematics and computer science. P(x)\}$ is equal to $\{y : $$ \{n \in \mathbb z | n = k^2 + l^2\text{ for some integers }k\text{ and }l\} $$ i don't know if $k$ and $l$ have to be equal for each pair of. It is specifically helpful in explaining the sets. Defenition of a set (8:41) number sets. In some treatments of the subject. Someone use : instead of |. For example, the set { 1, 2, 3, 4, 5, 6, 7, 8, 9 } list the elements. [1] specifying sets by member properties is.

Set builder notation Explanation and Examples

Builder notation is definitely not the best way here and you're unlikely. For example, the set { 1, 2, 3, 4, 5, 6, 7, 8, 9 } list the elements. It does not evaluate to a true/false condition which tells us in which case. We can see that each number in the set can be obtained by adding odd natural..

Set Builder Notation Cuemath

I want it to return an abbreviated set, just like the above example. It does not evaluate to a true/false condition which tells us in which case. If a given set builder notation is infinite, i want it to return abbreviated 'set exemplar' notation like {. It is specifically helpful in explaining the sets. It is a shorthand way of.

SetBuilder Notation. ppt download

\}$ is a useful way to represent a set which is characterized by some rule or property, nothing more. I have this following set notation: For example, the set { 1, 2, 3, 4, 5, 6, 7, 8, 9 } list the elements. If a given set builder notation is infinite, i want it to return abbreviated 'set exemplar' notation.

SetBuilder Notation YouTube

Autocomplete previous lesson complete and. $$ \{n \in \mathbb z | n = k^2 + l^2\text{ for some integers }k\text{ and }l\} $$ i don't know if $k$ and $l$ have to be equal for each pair of. Definition 1.let a and b be sets. An expression, a vertical bar, and a property. Describe the set of all odd numbers.

Set Builder Notation and Roster Method YouTube

It is specifically helpful in explaining the sets. The set builder notation $\{n\in\bbb n\mid n^2\}$ is meaningless, since $n^2$ is a term, not a formula. With sets it's whatever is the cleanest and least cumbersome method of specifying exactly what elements are in the set. $$ \{n \in \mathbb z | n = k^2 + l^2\text{ for some integers }k\text{.

Set Builder Notation & Interval Notation PDF Interval (Mathematics

Definition 1.let a and b be sets. I have this following set notation: P(x)\}$ is equal to $\{y : If a given set builder notation is infinite, i want it to return abbreviated 'set exemplar' notation like {. Builder notation is definitely not the best way here and you're unlikely.

Set Builder Notation YouTube

Builder notation is definitely not the best way here and you're unlikely. The union of a and b, denoted by a b, is a set that consists of the elements either in a or in b or in both. P(x)\}$ is equal to $\{y : An important use of predicates is in set builder notation. \exists x [y=f(x) \land p(x)]\}$.

Set Builder Notation Definition, Examples Set Builder Form

I have this following set notation: The set builder notation $\{n\in\bbb n\mid n^2\}$ is meaningless, since $n^2$ is a term, not a formula. I want it to return an abbreviated set, just like the above example. We’ll often want to talk about sets that cannot be described very well by listing the elements explicitly or by taking. Defenition of a.

Setbuilder notation Notations, Irrational numbers, Algebra

It is a shorthand way of writing the equivalent statement in logic,. Defenition of a set (8:41) number sets. It does not evaluate to a true/false condition which tells us in which case. For example, the set { 1, 2, 3, 4, 5, 6, 7, 8, 9 } list the elements. It is specifically helpful in explaining the sets.

Set builder notation Explanation and Examples

The same set could be. If a given set builder notation is infinite, i want it to return abbreviated 'set exemplar' notation like {. An expression, a vertical bar, and a property. Set builder notation is a mathematical notation that describes a set by stating all the properties that the elements in the set must satisfy. Defenition of a set.

If A Given Set Builder Notation Is Infinite, I Want It To Return Abbreviated 'Set Exemplar' Notation Like {.

\exists x [y=f(x) \land p(x)]\}$. In some treatments of the subject. $$ \{n \in \mathbb z | n = k^2 + l^2\text{ for some integers }k\text{ and }l\} $$ i don't know if $k$ and $l$ have to be equal for each pair of. For example, the set { 1, 2, 3, 4, 5, 6, 7, 8, 9 } list the elements.

It Does Not Evaluate To A True/False Condition Which Tells Us In Which Case.

Autocomplete previous lesson complete and. Describe the set of all odd numbers between $100$ and $200$ using set builder notation I have this following set notation: Set builder notation is a mathematical notation that describes a set by stating all the properties that the elements in the set must satisfy.

It Is Specifically Helpful In Explaining The Sets.

With sets it's whatever is the cleanest and least cumbersome method of specifying exactly what elements are in the set. $a = \{x | p(x)\}$ simply declares that 'the set a is the set of all x, such that x satisfies the predicate p'. Master discrete math, the backbone of mathematics and computer science. An important use of predicates is in set builder notation.

The Same Set Could Be.

Definition 1.let a and b be sets. An expression, a vertical bar, and a property. [1] specifying sets by member properties is. We can see that each number in the set can be obtained by adding odd natural.