Set Builder Notation With Infinity
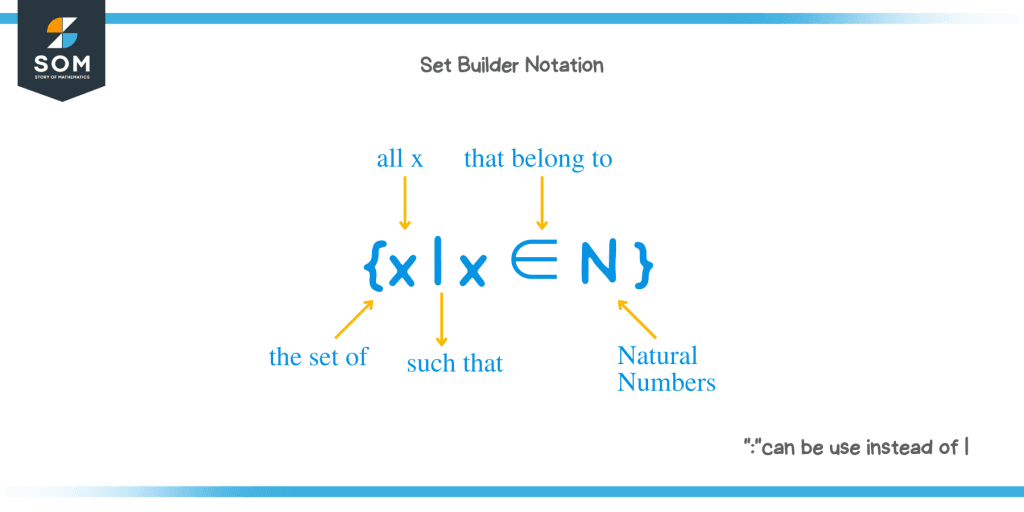
Set Builder Notation With Infinity - Are there better/cleaner more standard ways of representing xω in set builder notation? Sometimes there are an infinite amount of numbers that will satisfy an inequality, so rather than try to list off an infinite amount of numbers, we have developed some ways to describe very. {x|x≥ 4} {x | x ≥ 4}, which translates to “all real numbers x such that x is greater than or equal to 4.” notice that braces are used to indicate a set. [1] specifying sets by member properties is. To calculate it, you need: It's concise, allowing representation of large or infinite sets in a compact form; Sometimes there are an infinite amount of numbers that will satisfy an inequality, so rather than try to list off an infinite. In algebra, inequalities are used to describe large sets of solutions. Numbers such as real numbers, integers, natural numbers can be easily represented using the set. A shorthand used to write sets, often sets with an infinite number of elements. If you want to restrict an interval to a defined set of numbers following specific rules, you need the set builder notation or set builder form. Write the following in set builder notation. {x|x≥ 4} {x | x ≥ 4}, which translates to “all real numbers x such that x is greater than or equal to 4.” notice that braces are used to indicate a set. It's concise, allowing representation of large or infinite sets in a compact form; To calculate it, you need: X > 0} is read aloud, the set of all x such that x is greater than 0. Set builder notation offers several advantages: Numbers such as real numbers, integers, natural numbers can be easily represented using the set. An important use of predicates is in set builder notation. Sometimes there are an infinite amount of numbers that will satisfy an inequality, so rather than try to list off an infinite amount of numbers, we have developed some ways to describe very. Set builder notation offers several advantages: [1] specifying sets by member properties is. An important use of predicates is in set builder notation. It's precise, clearly defining properties that set members must. Sometimes there are an infinite amount of numbers that will satisfy an inequality, so rather than try to list off an infinite amount of numbers, we have developed. Set builder notation is the descriptive definition of the set. In mathematics, set builder notation is a way of representing a set of objects by a description of the properties that the objects have in common. In algebra, inequalities are used to describe large sets of solutions. {x|x≥ 4} {x | x ≥ 4}, which translates to “all real numbers. If you define ab as the set of. X > 0} is read aloud, the set of all x such that x is greater than 0. Sometimes there are an infinite amount of numbers that will satisfy an inequality, so rather than try to list off an infinite. To calculate it, you need: It takes the form\(\{x|\text{ statement about x}\}\). {x|x≥ 4} {x | x ≥ 4}, which translates to “all real numbers x such that x is greater than or equal to 4.” notice that braces are used to indicate a set. Here’s how to represent the set. [1] specifying sets by member properties is. An important use of predicates is in set builder notation. Set builder notation offers. X > 0} is read aloud, the set of all x such that x is greater than 0. It's concise, allowing representation of large or infinite sets in a compact form; Write the following in set builder notation. Numbers such as real numbers, integers, natural numbers can be easily represented using the set. If you define ab as the set. Sometimes there are an infinite amount of numbers that will satisfy an inequality, so rather than try to list off an infinite. {x|x≥ 4} {x | x ≥ 4}, which translates to “all real numbers x such that x is greater than or equal to 4.” notice that braces are used to indicate a set. Here’s how to represent the. X > 0} is read aloud, the set of all x such that x is greater than 0. Set builder notation is the descriptive definition of the set. If you define ab as the set of. In mathematics, set builder notation is a way of representing a set of objects by a description of the properties that the objects have. [1] specifying sets by member properties is. Write the following in set builder notation. Set builder notation offers several advantages: If you want to restrict an interval to a defined set of numbers following specific rules, you need the set builder notation or set builder form. Are there better/cleaner more standard ways of representing xω in set builder notation? Sometimes there are an infinite amount of numbers that will satisfy an inequality, so rather than try to list off an infinite. X > 0} is read aloud, the set of all x such that x is greater than 0. The most common symbols used in set. It takes the form\(\{x|\text{ statement about x}\}\) which is read as, “the set. Numbers such as real numbers, integers, natural numbers can be easily represented using the set. X > 0} is read aloud, the set of all x such that x is greater than 0. It's concise, allowing representation of large or infinite sets in a compact form; [1] specifying sets by member properties is. Set builder notation is the descriptive definition. Set builder notation offers several advantages: Sometimes there are an infinite amount of numbers that will satisfy an inequality, so rather than try to list off an infinite. Set builder notation is the descriptive definition of the set. An important use of predicates is in set builder notation. [1] specifying sets by member properties is. In algebra, inequalities are used to describe large sets of solutions. In mathematics, set builder notation is a way of representing a set of objects by a description of the properties that the objects have in common. A shorthand used to write sets, often sets with an infinite number of elements. It's concise, allowing representation of large or infinite sets in a compact form; If you define ab as the set of. Here’s how to represent the set. Write the following in set builder notation. If you want to restrict an interval to a defined set of numbers following specific rules, you need the set builder notation or set builder form. It takes the form\(\{x|\text{ statement about x}\}\) which is read as, “the set of all x. To calculate it, you need: We’ll often want to talk about sets that cannot be described very well by listing the elements explicitly or by taking unions,.Set Builder Notation Cuemath
SET BUILDER NOTATION YouTube
Set Theory Example Set Builder Notation YouTube
Set Builder Notation and Roster Method YouTube
Set builder notation Explanation and Examples
Interval Notation to SetBuilder Notation PreCalculus YouTube
SetBuilder Notation YouTube
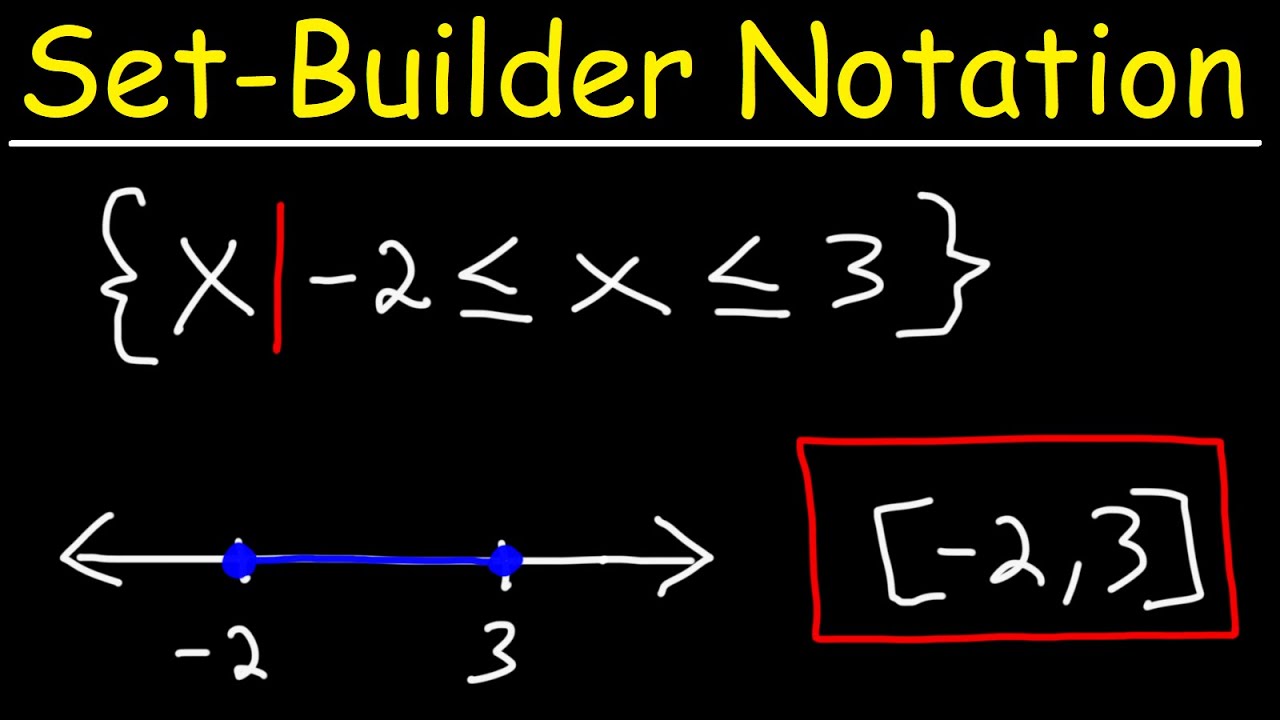
For the following exercises, write the interval in setbuilder notation
Set Builder Notation YouTube
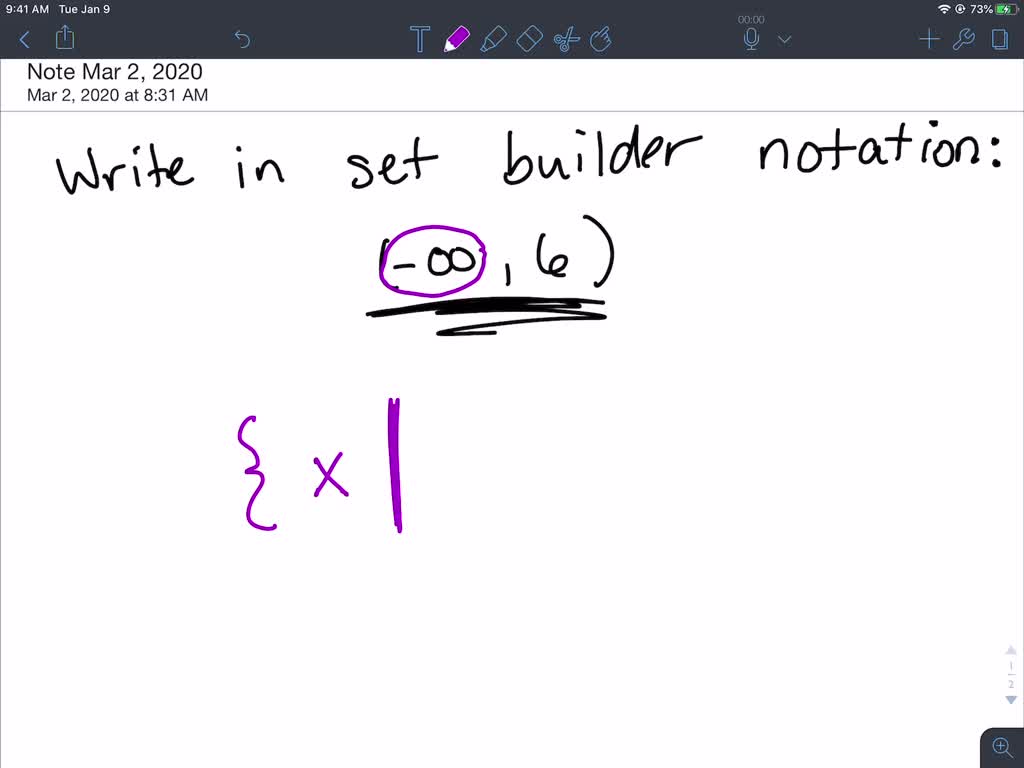
Set Builder Notation when Infinity is Involved YouTube
The Most Common Symbols Used In Set.
Sometimes There Are An Infinite Amount Of Numbers That Will Satisfy An Inequality, So Rather Than Try To List Off An Infinite Amount Of Numbers, We Have Developed Some Ways To Describe Very.
It's Precise, Clearly Defining Properties That Set Members Must.
Numbers Such As Real Numbers, Integers, Natural Numbers Can Be Easily Represented Using The Set.
Related Post: