Set Builder Notation Math Definition

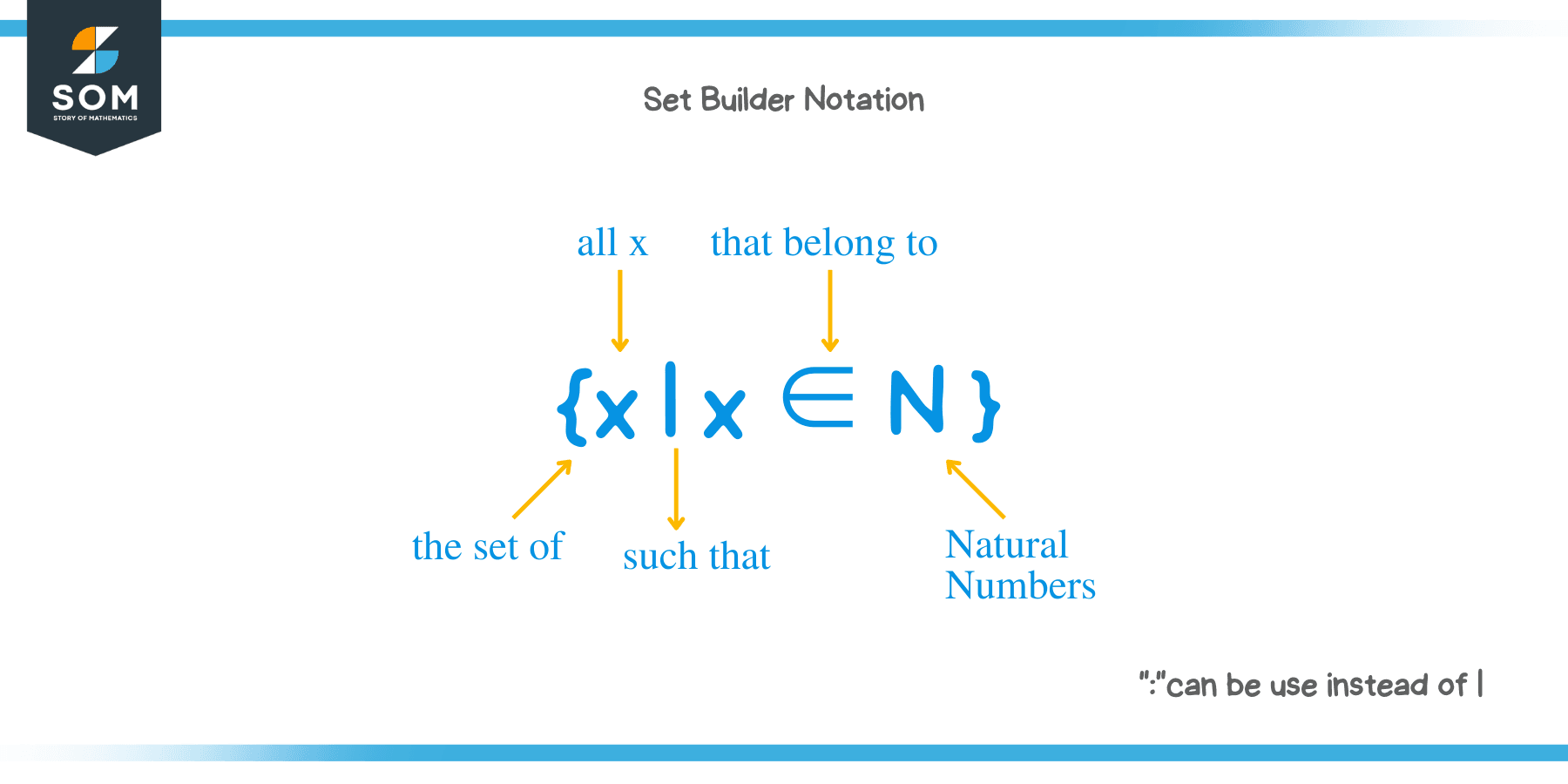
Set Builder Notation Math Definition - For example, look at x below: P (x) holds} or, {x | p (x) holds}, which is read as ‘the. We would read this aloud ``the set of a numbers of the form , where is an integer.. Set builder notation is a way to represent sets by using the condition satisfied by every element in the set or a property followed by every element of the set or a limitation on. The same set could be. Definition \(\pageindex{1}\) the union of sets \(a\) and \(b\), denoted \(a \cup b\), includes exactly the elements appearing in \(a\) or. Discrete mathematics for computer science (jin he). Set builder notation is a mathematical notation used to define a set in terms of properties that its elements must satisfy. Mathematics is working on the basis of. Denotes the set of all elements in which have the property.

We would read this aloud ``the set of a numbers of the form , where is an integer.. Set builder notation is a mathematical notation used to define a set in terms of properties that its elements must satisfy. This type of notation is typically used when the elements of a set. It's often useful to define a set in terms of the properties its elements are supposed to have. [2] [3] [4] these things are called elements or members of the set and are typically mathematical objects of any kind: In mathematics, a set is a. The same set could be. Mathematics is working on the basis of. In mathematics, a set is a collection of different [1] things; {x | x > 3 } recall that means “a member of”, or simply “in”.

PPT Basic Structures Sets, Functions, Sequences, Sums, and Matrices

{x | x > 3 } recall that means “a member of”, or simply “in”. For example, the set { 1, 2, 3, 4, 5, 6, 7, 8, 9 } list the elements. Set builder notation is an essential tool in the language of mathematics. It lets you precisely define and describe sets using mathematical symbols and logical expressions. This.

Set builder notation Explanation and Examples

[2] [3] [4] these things are called elements or members of the set and are typically mathematical objects of any kind: We would read this aloud ``the set of a numbers of the form , where is an integer.. For example, look at x below: {x | x > 3 } recall that means “a member of”, or simply “in”..

Set builder notation Explanation and Examples

It lets you precisely define and describe sets using mathematical symbols and logical expressions. In mathematics, a set is a. Is the special symbol for. The same set could be. Set builder notation is an essential tool in the language of mathematics.

Set Builder Notation Cuemath

[2] [3] [4] these things are called elements or members of the set and are typically mathematical objects of any kind: {x | x > 3 } recall that means “a member of”, or simply “in”. In this form, a set is described by a characterizing property p (x) of its elements x. This type of notation is typically used.

Set Builder Notation YouTube

It’s often used in mathematics to define sets in a concise way. In mathematics, set builder notation is a mathematical notation of describing a set by listing its elements or demonstrating its properties that its members must satisfy. Set builder notation is an essential tool in the language of mathematics. Is the special symbol for. Set builder notation is a.

Setbuilder notation Notations, Irrational numbers, Algebra

This is called set builder notation. P (x) holds} or, {x | p (x) holds}, which is read as ‘the. We would read this aloud ``the set of a numbers of the form , where is an integer.. In this form, a set is described by a characterizing property p (x) of its elements x. It’s often used in mathematics.

Set Builder Notation Definition, Examples Set Builder Form

Where (properties of x) is replaced by conditions. In mathematics, set builder notation is a mathematical notation of describing a set by listing its elements or demonstrating its properties that its members must satisfy. It lets you precisely define and describe sets using mathematical symbols and logical expressions. For example, look at x below: [2] [3] [4] these things are.

Set Builder Notation Math Definition Simple

It lets you precisely define and describe sets using mathematical symbols and logical expressions. Discrete mathematics for computer science (jin he). In such a case the set is described by {x : It’s often used in mathematics to define sets in a concise way. In mathematics, set builder notation is a mathematical notation of describing a set by listing its.

Set Builder Notation Cuemath

This type of notation is typically used when the elements of a set. In this form, a set is described by a characterizing property p (x) of its elements x. For example, look at x below: In mathematics, set builder notation is a mathematical notation of describing a set by listing its elements or demonstrating its properties that its members.

SetBuilder Notation YouTube

The same set could be. For example, look at x below: Is the special symbol for. Definition \(\pageindex{1}\) the union of sets \(a\) and \(b\), denoted \(a \cup b\), includes exactly the elements appearing in \(a\) or. Discrete mathematics for computer science (jin he).

In Mathematics, A Set Is A.

P (x) holds} or, {x | p (x) holds}, which is read as ‘the. For example, the set { 1, 2, 3, 4, 5, 6, 7, 8, 9 } list the elements. It lets you precisely define and describe sets using mathematical symbols and logical expressions. {x | x > 3 } recall that means “a member of”, or simply “in”.

Discrete Mathematics For Computer Science (Jin He).

Set builder notation is an essential tool in the language of mathematics. Set builder notation is a mathematical notation used to define a set in terms of properties that its elements must satisfy. [2] [3] [4] these things are called elements or members of the set and are typically mathematical objects of any kind: Definition \(\pageindex{1}\) the union of sets \(a\) and \(b\), denoted \(a \cup b\), includes exactly the elements appearing in \(a\) or.

Mathematics Is Working On The Basis Of.

Denotes the set of all elements in which have the property. In mathematics, a set is a collection of different [1] things; It's often useful to define a set in terms of the properties its elements are supposed to have. Where (properties of x) is replaced by conditions.

The Set Is Written In This Form:

We would read this aloud ``the set of a numbers of the form , where is an integer.. In this form, a set is described by a characterizing property p (x) of its elements x. In mathematics, set builder notation is a mathematical notation of describing a set by listing its elements or demonstrating its properties that its members must satisfy. In such a case the set is described by {x :